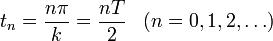Punto moviéndose sobre una parábola (G.I.A.)
De Laplace
1 Enunciado
Un punto inicialmente en reposo en la posición x = a, y = b,
describe la parábola 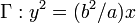 . Se conoce la
componente y de la aceleración: ay = − k2y, con k = cte.
Determina en función del tiempo la posición, velocidad y
aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto
tiempo tarda en alcanzarla?
. Se conoce la
componente y de la aceleración: ay = − k2y, con k = cte.
Determina en función del tiempo la posición, velocidad y
aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto
tiempo tarda en alcanzarla?
2 Solución
Podemos usar como parámetro de la curva la propia coordenada y. De este modo el vector que recorre los puntos de la curva es
![\vec{r}(t) = \Big[ \dfrac{a}{b^2}y(t)^2,y(t),0\Big]](/wiki/images/math/e/0/a/e0a4658e62bf51386b3f3c25ba1ffa0e.png)
La derivada y la aceleración son
![\begin{array}{l}
\vec{v}(t)=\dot{\vec{r}}(t) = \Big[
\dfrac{2a}{b^2}y\dot{y},\dot{y},0\Big]\\ \\
\vec{a}(t)=\dot{\vec{v}}(t) = \Big[ \dfrac{2a}{b^2}(\dot{y}^2+y\ddot{y}),\ddot{y},0\Big]
\end{array}](/wiki/images/math/b/d/e/bde9f398b48ee200beac00cce181844e.png)
El enunciado nos da la componente ay de la aceleración. Igualando a la expresión obtenida obtenemos la ecuación diferencial
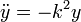
Puede comprobarse que las funciones cos(kt) y 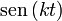 son
soluciones de esta ecuación. La solución más general puede escribirse
de la forma
son
soluciones de esta ecuación. La solución más general puede escribirse
de la forma
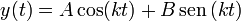
donde A y B son dos constantes. Su valor se determina a partir de las condiciones iniciales. El enunciado nos da la posición inicial y dice que se parte del reposo, es decir
![\begin{array}{l}
\vec{r}(0) = [a,b,0]\to y(0)=b\\ \\
\vec{v}(0) = [0,0,0]\to\dot{y}(0) = 0
\end{array}](/wiki/images/math/5/2/7/527cac1cfa39d1f4700c0f8a28a9830d.png)
La derivada de la solución general es
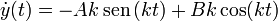
Aplicando las condiciones iniciales obtenemos las ecuaciones
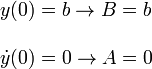
Por lo que la solución final es
Esto quiere decir que el valor de y oscila en el intervalo [ − b,b] con un período T = 2π / k. El vector de posición, la velocidad y la derivada se escriben
![\begin{array}{l}
\vec{r}(t) = \Big[a\cos^2(kt),b\cos(kt),0\Big]\\ \\
\vec{v}(t) = \Big[-ak\,\mathrm{sen}\,(2kt),-bk\,\mathrm{sen}\,(kt),0\Big]\\ \\
\vec{a}(t) = \Big[-2ak^2\cos(2kt),-bk^2\cos(kt),0\Big]
\end{array}](/wiki/images/math/2/3/9/239c1048efe9e8db3adc72a55ca0f22e.png)
Para obtener estas expresiones hemos usado la relaciones trigonométrica

2.1 Posiciones de reposo
Las posiciones de reposo se alcanzan cuando la velocidad es nula, es
decir, 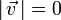 . El módulo es
. El módulo es

Hemos utilizado de nuevo la relación trigonométrica del seno del ángulo doble.
El módulo de la velocidad se anula cuando se cumple
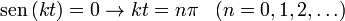
Por lo que los instantes de tiempo en que la velocidad es cero son