3.6. Oscilador armónico en el plano
De Laplace
Contenido |
1 Enunciado
Una partícula de masa m se encuentra sujeta a un resorte de constante k y longitud natural nula, que ejerce una fuerza
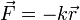
La posición inicial de la masa y su velocidad inicial son:
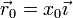
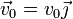
- Exprese el momento cinético de la partícula respecto al origen de coordenadas, O, y la energía mecánica de la partícula en función de x, y, z y sus derivadas temporales,
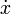 ,
, 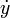 y
y 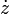 .
.
- Demuestre que las dos magnitudes anteriores son integrales primeras y evalúelas en función de las condiciones iniciales.
- Demuestre que el movimiento de esta partícula se restringe al plano OXY y que su velocidad areolar respecto al punto O es constante.
2 Momento cinético y energía
2.1 Momento cinético
Obtenemos el momento cinético multiplicando el vector de posición por la cantidad de movimiento. Separando en coordenadas cartesianas
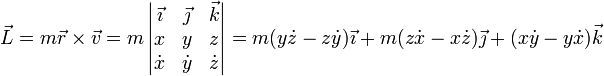
2.2 Energía mecánica
La energía mecánica es suma de la cinética
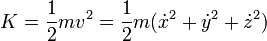
y la potencial
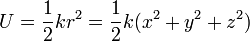
Resultando la energía
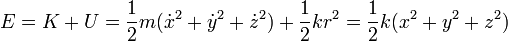
3 Integrales primeras
3.1 Momento cinético
La constancia del momento cinético es una consecuencia inmediata de que la fuerza producida por un oscilador armónico sea una fuerza central.
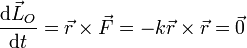
Podemos llegar a este resultado a partir de la expresión componente a componente. Así, para la componente z del momento cinético
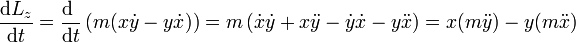
Sustituyendo aquí la ley de Hooke
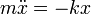
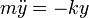
queda
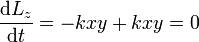
El valor del momento cinético lo obtenemos sustituyendo las condiciones iniciales
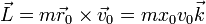
y, separando en sus componentes cartesianas
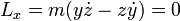
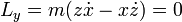
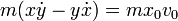
Al ser constante el momento cinético, la trayectoria es plana, siendo el plano de la órbita el definido por el vector de posición inicial (medido desde el centro de fuerzas) y la velocidad inicial.
En este caso tenemos que

El plano definido por estos dos vectores y el centro de fuerzas es el plano OXY, por lo que la trayectoria se limita a este plano.
4 Valor del momento cinético
Al estar limitada la trayectoria al plano OXY, el momento cinético posee solo componente en la dirección de OZ. la expresión de \vec{L} es
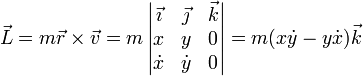
Podemos demostrar directamente la constancia de esta cantidad derivándola respecto al tiempo
De la constancia del momento cinético deducimos que la partícula no puede llegar a
detenerse en ningún momento (cosa que sí ocurre en el oscilador armónico en una
dimensión), ya que no podemos hacer simultáneamente 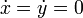 .
.
Por una razón análoga vemos que el oscilador no puede pasar por el origen de coordenadas, sino que habrá un valor mínimo de la distancia al origen.
5 Energía mecánica
La energía mecánica de un oscilador armónico es la suma de la cinética más la correspondiente energía potencial
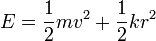
que para el caso bidimensional queda
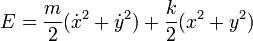
Demostramos que es una integral primera derivándola respecto al tiempo
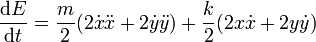
Agrupando términos y aplicando de nuevo la ley de Hooke
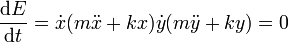
Por tanto, la energía mecánica es una constante de movimiento. Su valor lo obtenemos igualándola a su valor inicial