Entrar Página Discusión Historial Go to the site toolbox

3.5. Partícula en el interior de un tubo

De Laplace

Contenido

1 Enunciado

Una partícula de masa m se encuentra contenida en el interior de un tubo estrecho, el cual gira con velocidad angular ω, uniformemente en torno a un eje perpendicular al del tubo, de forma que la posición de la partícula puede escribirse como

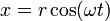
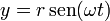
x = r \cos(\omega t)\,        y= r\,\mathrm{sen}(\omega t)

con r = r(t) la posición de la partícula a lo largo del tubo, función que hay que determinar.

  1. Halle la ecuación de movimiento para r(t) sabiendo que el tubo no puede ejercer fuerza en la dirección longitudinal.
  2. Compruebe que
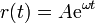
    r(t) =A\mathrm{e}^{\omega t}\,
    es una solución de la ecuación de movimiento anterior.
  3. Para esta solución particular
    1. Calcule la fuerza ejercida por el tubo en cada instante.
    2. Halle la potencia desarrollada por el tubo sobre la partícula.
    3. Calcule el trabajo realizado sobre la partícula durante el tiempo que emplea en pasar de r = b a r = 2b.
    4. Calcule el incremento de energía cinética de la partícula en el mismo intervalo y compruebe que se verifica el teorema de las fuerzas vivas o de la energía.

2 Ecuación diferencial

Calculamos la aceleración de la partícula derivando dos veces respecto al tiempo

\begin{array}{rcl} \dot{x} & = & \dot{r}\cos(\omega t) - r\omega\,\mathrm{sen}(\omega t) \\ \dot{y} & = & \dot{r}\,\mathrm{sen}(\omega t) + r\omega\cos(\omega t) \\ \ddot{x} & = & (\ddot{r}-\omega^2r)\cos(\omega t)-2\omega\dot{r}\,\mathrm{sen}(\omega t)\\ \ddot{y} & = & (\ddot{r}-\omega^2r)\mathrm{sen}(\omega t)+2\omega\dot{r}\cos(\omega t) \end{array}

La segunda ley de Newton nos dice que

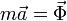
m\vec{a}=\vec{\Phi}

pero dado que la fuerza de reacción vincular no puede ir en la dirección radial, debe cumplirse que

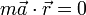
m\vec{a}\cdot\vec{r}=0

Desarrollando este producto escalar queda

0 = \vec{a}\cdot\vec{r}=\ddot{x}x+\ddot{y}y=r(\ddot{r}-\omega^2r)

Para que este producto sea nulo o bien r = 0 y la partícula se queda en equilibrio en la posición central del tubo, o se cumple la ecuación diferencial

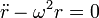
\ddot{r}-\omega^2r = 0

Esta es la ecuación que determina cómo varía la distancia radial con el tiempo.

3 Solución particular

Derivando dos veces

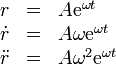
\begin{array}{rcl} r & = & A\mathrm{e}^{\omega t}\\ \dot{r} & = & A\omega\mathrm{e}^{\omega t}\\ \ddot{r} & = & A\omega^2\mathrm{e}^{\omega t} \end{array}

y sustituyendo

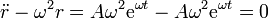
\ddot{r}-\omega^2r = A\omega^2\mathrm{e}^{\omega t} - A\omega^2\mathrm{e}^{\omega t} = 0

luego efectivamente es una solución particular de esta ecuación.

3.1 Fuerza de reacción

Obtenemos la fuerza de reacción vincular sustituyendo en la segunda ley de Newton

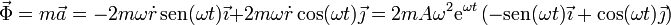
\vec{\Phi}=m\vec{a}=-2m\omega\dot{r}\,\mathrm{sen}(\omega t)\vec{\imath}+ 2m\omega\dot{r}\cos(\omega t)\vec{\jmath} = 2m A\omega^2\mathrm{e}^{\omega t} \left(-\mathrm{sen}(\omega t)\vec{\imath}+ \cos(\omega t)\vec{\jmath}\right)

3.2 Potencia desarrollada

La potencia desarrollada por la fuerza de reacción es el producto de ésta por la velocidad de la partícula. Esta velocidad vale

\vec{v} = \dot{x}\vec{\imath}+\dot{y}\vec{\jmath} = A\omega\mathrm{e}^{\omega t}\left((\cos(\omega t)-\mathrm{sen}(\omega t))\vec{\imath}+(\mathrm{sen}(\omega t)+\cos(\omega t))\vec{\jmath}\right)

Esta velocidad no es puramente radial, sino que forma un ángulo de 45° con el tubo.

Hallamos el producto escalar y resulta

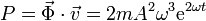
P=\vec{\Phi}\cdot\vec{v}= 2m A^2\omega^3\mathrm{e}^{2\omega t}

3.3 Trabajo en un intervalo

El trabajo realizado en un intervalo es

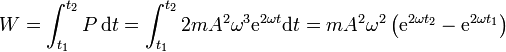
W = \int_{t_1}^{t_2}P\,\mathrm{d}t = \int_{t_1}^{t_2} 2mA^2\omega^3\mathrm{e}^{2\omega t}\mathrm{d}t = mA^2\omega^2\left(\mathrm{e}^{2\omega t_2}-\mathrm{e}^{2\omega t_1}\right)

En este caso, t_1 y t_2 son tales que

b = A \mathrm{e}^{\omega t_1}\qquad 2b = A \mathrm{e}^{\omega t_2}

por lo que el trabajo en este desplazamiento vale

W = mω2((2b)2 − b2) = 3mω2b2

4 Energía cinética

La energía cinética en cada instante para esta solución es, sustituyendo,

K = \frac{1}{2}m(\dot{x}^2+\dot{y}^2) = m\omega^2A^2\mathrm{e}^{2\omega t} 

= m\omega^2 r^2

Por tanto, el incremento entre r=b y r=2b vale

\Delta K = m\omega^2(4b^2-b^2) = 3m\omega^2b^2

en completo acuerdo con el trabajo de las fuerzas vivas.

Tenemos entonces que la partícula se va acelerando y ganando energía cinética. El trabajo necesario para este incremento lo realiza la fuerza de reacción vincular, que en este caso no es puramente normal a la trayectoria, sino que forma un cierto ángulo con ella.

Obtenido de "http://tesla.us.es/wiki/index.php/3.5._Part%C3%ADcula_en_el_interior_de_un_tubo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace