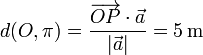Distancia de un punto a un plano (G.I.A.)

De Laplace

Revisión a fecha de 12:11 14 oct 2010; Pedro (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Encuentra la ecuación del plano perpendicular al vector libre 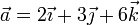$\vec{a} = 2\vec{\imath} +3\vec{\jmath} + 6\vec{k}$ y que contiene a un punto $P$ , cuya posición respecto del origen de un sistema de referencia $O X Y Z$ viene dada por el radio vector 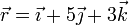$\vec{r}=\vec{\imath}+5\vec{\jmath}+3\vec{k}$ . Calcula la distancia que separa al origen $O$ de dicho plano (todas las distancias están dadas en metros).

2 Solución

Tenemos el vector normal al plano, $\vec{a}$ y el vector de posición del punto $P$

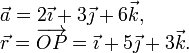
$\begin{array}{l} \vec{a} = 2\vec{\imath} + 3\vec{\jmath} + 6\vec{k},\\ \vec{r} =\overrightarrow{OP} = \vec{\imath} + 5\vec{\jmath} + 3\vec{k}. \end{array}$

Sea $Q (x, y, z)$ un punto cualquiera del plano $π$ . Entonces el vector 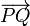$\overrightarrow{PQ}$ debe ser perpendicular al vector $\vec{a}$ , esto es