No Boletín - Rotación y traslación terrestres
De Laplace
1 Enunciado
La Tierra rota uniformemente con respecto a su eje con velocidad angular ω constante. Encuentre en función de la latitud λ, la velocidad y la aceleración de un punto sobre la superficie terrestre, debidas a dicha rotación (radio de la Tierra: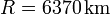 
)
Compare los módulos de los valores anteriores para el caso de un punto en el Ecuador, con los correspondientes al movimiento de traslación alrededor del Sol (distancia Tierra-Sol aproximadamente constante e igual a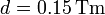 
).
2 Movimiento de rotación
Un punto en un movimiento de rotación uniforme describe un movimiento circular uniforme, con velocidad y aceleración
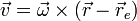
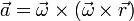
siendo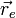 
un punto del eje de rotación, que en el caso de la rotación
terrestre podemos tomar el centro de la Tierra, considerado asimismo como origen de
coordenadas.
2.1 Velocidad
La dirección de la velocidad es tangente a la superficie en cada punto y dirigida hacia el este. El módulo de esta velocidad es
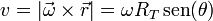
Aquí θ es el ángulo que forman la velocidad angular, que va en la dirección del eje terrestre, con el vector de posición de cada punto. Este ángulo es la colatitud, complementaria de la latitud
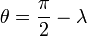
lo que nos da la celeridad
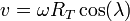
Aquí, RT es el radio terrestre, mientras que ω se obtiene a partir del periodo de rotación terrestre
