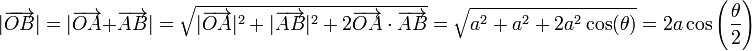2.3. Movimiento de partícula sujeta de un hilo
De Laplace
Revisión a fecha de 10:01 5 oct 2010; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
Una barra rígida AB de longitud a se mueve en un plano vertical OXY, manteniendo su extremo A articulado en un punto del eje horizontal de coordenadas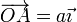 
, y verificando la ley horaria θ(t) = 2ωt, con 
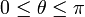y siendo ω = cte. Un hilo inextensible de longitud 2a tiene uno de sus extremos conectado al origen del sistema de referencia (punto O), mientras que del otro cuelga una partícula P que mantiene al hilo siempre tenso. El hilo se apoya sobre una pequeña polea de radio despreciable situada en el extremo B de la barra, de forma que el tramo 
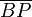permanece siempre paralelo al eje OY (ver figura). Se pide:
- Ecuaciones horarias del punto P,
.
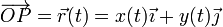- Instante del tiempo tM en que la partícula alcanza su altura máxima.
- Radio de curvatura de la trayectoria seguida por P, en el instante considerado en el apartado anterior.
2 Ecuaciones horarias
La posición del punto P puede escribirse como suma de tres vectores
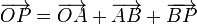
donde
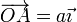
y
El vector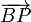 
es vertical hacia abajo y con un módulo igual a
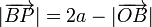
siendo
