Movimiento cicloidal

De Laplace

Revisión a fecha de 16:02 4 oct 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Velocidad en función de la posición
3 Solución particular
4 Velocidad y aceleración
- 4.1 Velocidad
- 4.2 Aceleración
5 Celeridad y ley horaria
6 Componentes intrínsecas de la aceleración

1 Enunciado

Un punto de un disco de radio $b$ que rueda a velocidad constante sobre una superficie plana en $y = 0$ tiene por velocidad

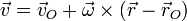
$\vec{v}=\vec{v}_O+\vec{\omega}\times\left(\vec{r}-\vec{r}_O\right)$

donde

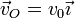
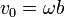
$\vec{v}_O=v_0\vec{\imath}$ $\vec{\omega}=-\omega\vec{k}$ $v_0=\omega b\,$

son la velocidad de traslación del centro del disco y la velocidad angular de rotación alrededor de él, respectivamente.

Halle la expresión de la velocidad en función de las coordenadas de un punto del disco y del tiempo.
Pruebe que las ecuaciones horarias

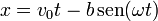
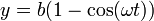
$x = v_0 t -b\,\mathrm{sen}(\omega t)$ $y = b(1-\cos(\omega t))\,$

son soluciones de las ecuaciones obtenidas en el primer apartado para un punto del borde del disco.

Para el movimiento anterior, calcule la velocidad y la aceleración instantáneas
Halle la celeridad instantánea, así como la ley horaria $s (t)$ para intervalo $0 < t < T$ con T el periodo de revolución del disco.
Determine las componentes intrínsecas de la aceleración, el radio de curvatura y la posición del centro de curvatura para el mismo periodo anterior.

2 Velocidad en función de la posición

El centro del disco avanza uniformemente, de forma que su posición en cada instante es, tomando $y = 0$ como el plano de rodadura

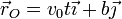
$\vec{r}_O=v_0t\vec{\imath}+b\vec{\jmath}$

La posición de un punto cualquiera del disco es

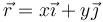
$\vec{r}=x\vec{\imath}+y\vec{\jmath}$

Sustituyendo en la expresión de la velocidad obtenemos

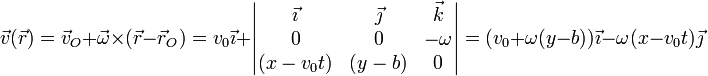
$\vec{v}(\vec{r})=\vec{v}_O+\vec{\omega}\times(\vec{r}-\vec{r}_O)=v_0\vec{\imath}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & -\omega \\ (x-v_0t) & (y-b) & 0\end{matrix}\right|=(v_0+\omega(y-b))\vec{\imath} - \omega(x-v_0t)\vec{\jmath}$

Si separamos en componentes obtenemos, para las derivadas respecto al tiempo de cada componente

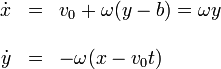
$\begin{array}{rcl}\dot{x} & = & v_0 + \omega(y-b) = \omega y \\ && \\ \dot{y} & = & -\omega(x-v_0t)\end{array}$

donde hemos aplicado que $v 0 = ω b$ .

3 Solución particular

El sistema anterior

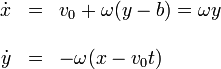
$\begin{array}{rcl}\dot{x} & = & v_0 + \omega(y-b) = \omega y \\ && \\ \dot{y} & = & -\omega(x-v_0t)\end{array}$

nos relaciona la velocidad (esto es, cómo cambia la posición con el tiempo) como función de la posición. Esto es, para determinar la posición necesitamos conocer la posición. Esta aparente circularidad (que no es tal, ya que en realidad es, para conocer la posición en $t + d t$ necesitamos conocer la posición en $t$ ) es lo que se conoce como una ecuación diferencial. Existen toda una serie de técnicas estándar para resolver este tipo de ecuaciones, pero aquí nos limitaremos a comprobar que unas determinadas ecuaciones horarias son soluciones de ellas.

Tenemos las ecuaciones horarias

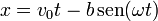
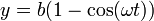
$x = v_0 t -b\,\mathrm{sen}(\omega t)$ $y = b(1-\cos(\omega t))\,$

Veamos en primer lugar que corresponden a un punto del borde del disco. Hallamos la posición relativa al centro del disco

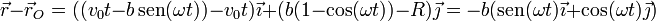
$\vec{r}-\vec{r}_O = ((v_0 t -b\,\mathrm{sen}(\omega t))-v_0t)\vec{\imath}+(b(1-\cos(\omega t))-R)\vec{\jmath}=-b(\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath})$

El módulo de este vector es

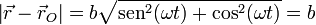
$\left|\vec{r}-\vec{r}_O\right| = b\sqrt{\mathrm{sen}^2(\omega t)+\cos^2(\omega t)} = b$

Luego efectivamente se encuentra sobre la circunferencia exterior.

Derivamos ahora respecto al tiempo para calcular las componentes cartesianas de la velocidad

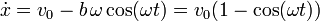
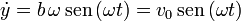
$\dot{x}=v_0-b\,\omega\cos(\omega t) = v_0(1-\cos(\omega t))$ $\dot{y}=b\,\omega\,\mathrm{sen}\,(\omega t) = v_0\,\mathrm{sen}\,(\omega t)$

Es inmediato comprobar que esta solución cumple las ecuaciones diferenciales enunciadas anteriormente:

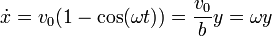
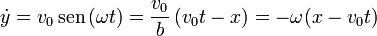
$\dot{x}=v_0(1-\cos(\omega t)) = \frac{v_0}{b}y=\omega y$ $\dot{y}=v_0\,\mathrm{sen}\,(\omega t) = \frac{v_0}{b}\left(v_0t-x\right) = -\omega(x-v_0t)$

4 Velocidad y aceleración

4.1 Velocidad

Las componentes de la velocidad ya las hemos calculado. Expresándolas en forma vectorial

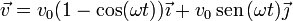
$\vec{v}=v_0(1-\cos(\omega t))\vec{\imath}+v_0\,\mathrm{sen}\,(\omega t)\vec{\jmath}$

4.2 Aceleración

Derivando de nuevo

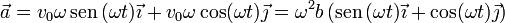
$\vec{a}=v_0\omega\,\mathrm{sen}\,(\omega t)\vec{\imath}+v_0\omega\cos(\omega t)\vec{\jmath}=\omega^2b\left(\mathrm{sen}\,(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath}\right)$

Vemos que resulta una aceleración de módulo constante, pero dirección variable. por ello el movimiento no es uniformemente acelerado.

5 Celeridad y ley horaria

Usando las relaciones trigonométricas

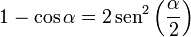
$1-\cos\alpha = 2\,\mathrm{sen}^2\left(\frac{\alpha}{2}\right)$ $\mathrm{sen}\,\alpha = 2\,\mathrm{sen}\left(\frac{\alpha}{2}\right)\cos\left(\frac{\alpha}{2}\right)$

podemos escribir la velocidad en la forma

$\vec{v}=2v_0\,\mathrm{sen}\left(\frac{\omega t}{2}\right)\left(\mathrm{sen}\left(\frac{\omega t}{2}\right)\vec{\imath}+\cos\left(\frac{\omega t}{2}\right)\vec{\jmath}\right)$

puesto que el vector entre paréntesis es unitario es claro que la celeridad y el vector tangente valen

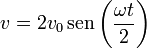
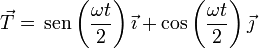
$v = 2v_0\,\mathrm{sen}\left(\frac{\omega t}{2}\right)$ $\vec{T}=\,\mathrm{sen}\left(\frac{\omega t}{2}\right)\vec{\imath}+\cos\left(\frac{\omega t}{2}\right)\vec{\jmath}$

Conocida la celeridad, podemos obtener el parámetro arco como función del tiempo

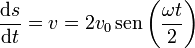
$\frac{\mathrm{d}s}{\mathrm{d}t}=v=2v_0\,\mathrm{sen}\left(\frac{\omega t}{2}\right)$ $\Rightarrow$ $s = \int_0^t v\,\mathrm{d}t = \left.-4\frac{v_0}{\omega}\cos\left(\frac{\omega t}{2}\right)\right|_0^t = 4b\left(1-\cos\left(\frac{\omega t}{2}\right)\right)$

La distancia total recorrida en una vuelta completa es

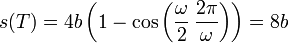
$s(T) = 4b\left(1-\cos\left(\frac{\omega}{2}\,\frac{2\pi}{\omega}\right)\right)=8b$

Vemos que aunque la rueda avanza una distancia $2\pi b\simeq 6.28b$ , un punto del borde recorre una distancia mayor, ya que no solo se mueve horizontalmente, sino también en vertical.

6 Componentes intrínsecas de la aceleración

6.1 Aceleración tangencial

El módulo de la aceleración tangencial es la derivada temporal de la celeridad

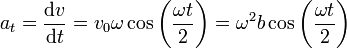
$a_t=\frac{\mathrm{d}v}{\mathrm{d}t}=v_0\omega\cos\left(\frac{\omega t}{2}\right)=\omega^2b\cos\left(\frac{\omega t}{2}\right)$

En forma vectorial

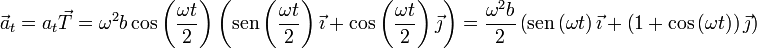
$\vec{a}_t=a_t\vec{T}=\omega^2b\cos\left(\frac{\omega t}{2}\right)\left(\mathrm{sen}\left(\frac{\omega t}{2}\right)\vec{\imath}+\cos\left(\frac{\omega t}{2}\right)\vec{\jmath}\right)=\frac{\omega^2b}{2}\left(\mathrm{sen}\left(\omega t\right)\vec{\imath}+\left(1+\cos\left(\omega t\right)\right)\vec{\jmath}\right)$

6.2 Aceleración normal

Hallamos la aceleración normal restando la tangencial de la completa y resulta

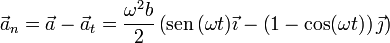
$\vec{a}_n=\vec{a}-\vec{a}_t=\frac{\omega^2b}{2}\left(\mathrm{sen}\,(\omega t)\vec{\imath}-\left(1-\cos(\omega t)\right)\vec{\jmath}\right)$

Empleando de nuevo las mismas relaciones trigonométricas

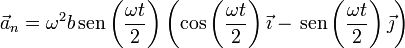
$\vec{a}_n=\omega^2b\,\mathrm{sen}\left(\frac{\omega t}{2}\right)\left(\cos\left(\frac{\omega t}{2}\right)\vec{\imath}-\,\mathrm{sen}\left(\frac{\omega t}{2}\right)\vec{\jmath}\right)$

de donde hallamos el vector normal

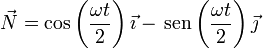
$\vec{N}=\cos\left(\frac{\omega t}{2}\right)\vec{\imath}-\,\mathrm{sen}\left(\frac{\omega t}{2}\right)\vec{\jmath}$

y el módulo de la aceleración normal

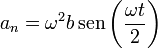
$a_n=\omega^2b\,\mathrm{sen}\left(\frac{\omega t}{2}\right)$

Podíamos haber llegado a este módulo directamente a partir de los de la aceleración completa y la aceleración tangencial, empleando el teorema de Pitágoras

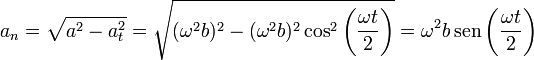
$a_n = \sqrt{a^2-a_t^2}=\sqrt{(\omega^2b)^2-(\omega^2b)^2\cos^2\left(\frac{\omega t}{2}\right)}=\omega^2b\,\mathrm{sen}\left(\frac{\omega t}{2}\right)$

6.3 Radio de curvatura

Conocidas la celeridad y la aceleración normal tenemos el radio de curvatura

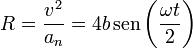
$R=\frac{v^2}{a_n}=4b\,\mathrm{sen}\left(\frac{\omega t}{2}\right)$

Este radio es nulo en el punto inicial, en el que la trayectoria tiene un vértice, crece hasta un valor máximo $4 b$ y vuelve a disminuir a cero en el siguiente vértice.

6.4 Centro de curvatura

Prolongando en la dirección del vector normal llegamos a

$\vec{r}_c=\vec{r}+ R\vec{N}= \left(v_0 t +b\,\mathrm{sen}(\omega t)\right)\vec{\imath}-b(1-\cos(\omega t))\vec{\jmath}$

Este resultado indica que la curva formada por los centros de curvatura (lo que se denomina la evoluta) es otra cicloide.

Movimiento cicloidal

De Laplace

Contenido

1 Enunciado

2 Velocidad en función de la posición

3 Solución particular

4 Velocidad y aceleración

4.1 Velocidad

4.2 Aceleración

5 Celeridad y ley horaria

6 Componentes intrínsecas de la aceleración

6.1 Aceleración tangencial

6.2 Aceleración normal

6.3 Radio de curvatura

6.4 Centro de curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES