Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática del punto material (G.I.T.I.)

De Laplace

Contenido

1 Ejemplo de movimiento rectilíneo

Una partícula efectúa un movimiento rectilíneo tal que si x(t) es la posición a lo largo de la recta y v(t) la componente de la velocidad en dicha dirección, se cumple en todo instante

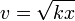
v = \sqrt{k x}
  1. Determine la aceleración en cada punto. ¿Qué tipo de movimiento efectúa la partícula?
  2. Si en t = 0 la partícula se encuentra en x = x0, ¿cuál es su posición en cualquier instante posterior?

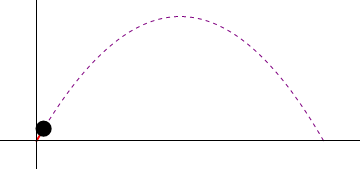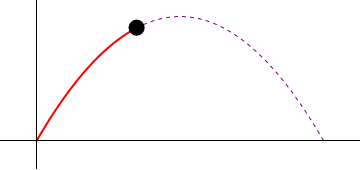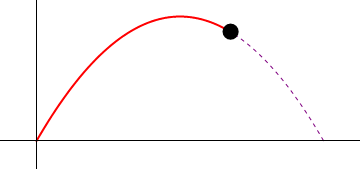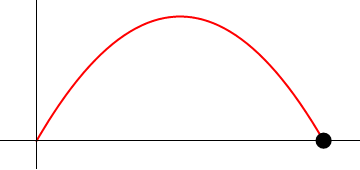
2 Cinemática del tiro parabólico

Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante

\vec{a}(t)=-g\vec{k}

una posición inicial nula (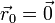\vec{r}_0=\vec{0}) y una velocidad inicial que forma un ángulo α con la horizontal y tiene rapidez inicial v0.

  1. Determine el vector de posición, la velocidad y la aceleración en cada instante.
  2. Calcule la celeridad y el vector tangente en el instante inicial, en el instante en que se encuentra a mayor altura y en el momento en que vuelve a impactar con el suelo.
  3. Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los tres instantes anteriores.
  4. Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria.
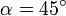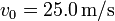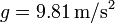  5. Para este mismo punto, halle las componentes intrínsecas de la velocidad y la aceleración, así como el radio de curvatura, si \alpha = 45^\circ, v_0=25.0\,\mathrm{m}/\mathrm{s} y g=9.81\,\mathrm{m}/\mathrm{s}^2.

3 Ejemplo de movimiento plano en 3D

Una partícula describe un movimiento según la ecuación horaria

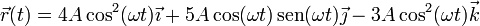
\vec{r}(t) = 4A\cos^2(\omega t)\vec{\imath}+5A\cos(\omega t)\,\mathrm{sen}(\omega t)\vec{\jmath}-3A\cos^2(\omega t)\vec{k}
  1. Calcule la velocidad y la aceleración instantáneas de este movimiento.
  2. Determine el parámetro arco como función del tiempo y escriba la ecuación de la trayectoria como función del parámetro arco.
  3. Calcule el triedro de Frenet asociado a la trayectoria en cada instante, así como las componentes intrínsecas de la aceleración
  4. Halle el radio de curvatura y la posición del centro de curvatura en cada instante.

4 Movimiento circular no uniforme

Una partícula describe un movimiento según la ecuación horaria

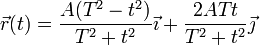
\vec{r}(t) = \frac{A(T^2-t^2)}{T^2+t^2}\vec{\imath}+\frac{2ATt}{T^2+t^2}\vec{\jmath}
  1. Calcule la aceleración y la velocidad instantáneas de este movimiento.
  2. Determine el parámetro arco como función del tiempo y escriba la ecuación de la trayectoria como función del parámetro arco.
  3. Calcule los vectores tangente y normal a la trayectoria en cada instante, así como las componentes intrínsecas de la aceleración.
  4. Halle el radio de curvatura y la posición del centro de curvatura en cada instante.

5 Ejemplo de movimiento helicoidal

Una partícula se mueve a lo largo de la hélice descrita por la ecuación paramétrica

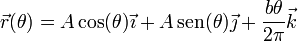
\vec{r}(\theta)=A\cos(\theta)\vec{\imath}+A\,\mathrm{sen}(\theta)\vec{\jmath}+\frac{b\theta}{2\pi}\vec{k}

donde A y b son constantes conocidas. El movimiento de la partícula sigue la ley horaria

θ(t) = Ω0t + βt2

donde Ω0 y β son constantes conocidas.

  1. Determine el parámetro arco de la hélice descrita, como función del parámetro θ y del tiempo.
  2. Halle la rapidez del movimiento.
  3. Calcule la componente tangencial de la aceleración de la partícula en todo instante.
  4. Para el instante t = 0 calcule la velocidad y la aceleración de la partícula.
  5. Para el mismo instante, halle los vectores del triedro de Frenet, así como el radio de curvatura de la partícula y su aceleración normal.

6 Espiral logarítmica

Una partícula recorre la espiral logarítmica de ecuación

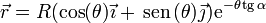
\vec{r} = R (\cos(\theta)\vec{\imath}+\,\mathrm{sen}\,(\theta)\vec{\jmath})\mathrm{e}^{-\theta\,\mathrm{tg}\,\alpha}

donde R y α son constantes. El movimiento es uniforme a lo largo de la curva, con celeridad constante v0. En el instante inicial la partícula se encuentra en θ = 0

  1. Determine la ley horaria θ = θ(t).
  2. Calcule el tiempo que tarda en llegar a 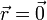\vec{r}=\vec{0}. ¿Cuántas vueltas da para ello?
  3. Halle el vector aceleración y sus componentes intrínsecas en cada punto de la trayectoria.
  4. Determine la posición de los centros de curvatura de este movimiento.

7 Evolvente de una circunferencia

La \emph{evolvente} de una circunferencia es la curva plana que se obtiene cuando se desenrolla un hilo tenso de un carrete circular. Suponga que se tiene una bobina de radio $A$ que se va desenrollando a ritmo constante, de forma que el punto de contacto del hilo con el carrete forma un ángulo θ = ωt con el punto inicial. Una partícula material se encuentra en el extremo del hilo, moviéndose con este extremo a medida que el hilo se va desenrollando.

  1. Determine el vector de posición de la partícula.
  2. Calcule la velocidad y la aceleración de la partícula.
  3. Determine la ley horaria s = s(t).
  4. Halle los vectores tangente y normal a la trayectoria.
  5. Halle el radio de curvatura y el centro de curvatura.

8 Movimiento cicloidal

Un punto de un disco que rueda a velocidad constante sobre una superficie plana en y = 0 tiene por velocidad

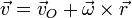
\vec{v}=\vec{v}_O+\vec{\omega}\times\vec{r}

donde

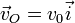
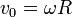
\vec{v}_O=v_0\vec{i}        \vec{\omega}=-\omega\vec{k}        v_0=\omega R\,

son la velocidad de traslación del centro del disco y la velocidad angular de rotación alrededor de él, respectivamente.

  1. Halle la expresión de la velocidad en función de las coordenadas de un punto del disco y del tiempo.
  2. Pruebe que las ecuaciones horarias
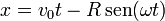
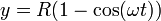
x = v_0 t -R\,\mathrm{sen}(\omega t)        y = R(1-\cos(\omega t))\,
son soluciones de las ecuaciones obtenidas en el primer apartado para un punto del borde del disco.
  1. Para el movimiento anterior, calcule la velocidad y la aceleración instantáneas
  2. Halle la celeridad instantánea, así como la ley horaria s(t) para intervalo 0 < t < T con T el periodo de revolución del disco.
  3. Determine las componentes intrínsecas de la aceleración, el radio de curvatura y la posición del centro de curvatura para el mismo periodo anterior.
Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_del_punto_material_(G.I.T.I.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace