1.7. Seno y coseno de una diferencia

De Laplace

1 Enunciado

A partir del producto escalar y del vectorial de dos vectores del plano, con módulo unidad, demuestre las fórmulas trigonométricas para el coseno y el seno de una diferencia de dos ángulos.

2 Coseno de una diferencia

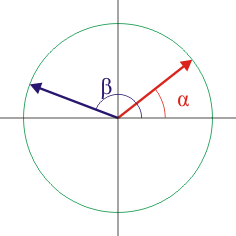
Consideremos los dos vectores 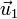y 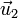, ambos de módulo unidad, y que forman ángulos α y β con el eje X, respectivamente.

El producto escalar de los dos vectores es igual a

Por otro lado, las componentes de estos vectores en la base canónica son

        

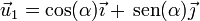
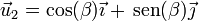
de forma que su producto escalar también se puede calcular como la suma de los productos de las componentes

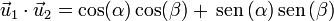
Igualando las dos expresiones para el producto escalar