1.2. Paralelogramo en cuadrilátero
De Laplace
Revisión a fecha de 00:24 16 sep 2010; Antonio (Discusión | contribuciones)
1 Enunciado
Sea ABCD un cuadrilátero arbitrario. Demuestre, usando el álgebra vectorial, que los puntos medios de sus cuatro lados constituyen los vértices de un paralelogramo.
2 Solución
Sea O el origen de coordenadas. En ese caso los vectores de posición de los vértices son 
, 
, 
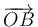y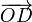 
. Las posiciones de los puntos medios E, F, G y H se encuentran en
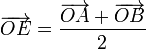
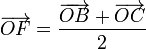
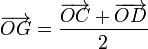
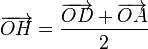
Para demostrar que estos cuatro puntos forman un paralelogramo, debemos probar que sus lados son paralelos dos a dos. El vector que une E y F es
