Incertidumbre en los datos
De Laplace
Contenido |
1 Introducción
En Ingeniería y en las Ciencias Experimentales, a diferencia de en Matemáticas, la mayoría de las cantidades no son conocidas exactamente (salvo que se trate de factores numéricos como 2, 10 o π). Los datos y resultados de cálculos físicos proceden en última instancia de la experiencia y por tanto están sujetos a incertidumbre.
Así, por ejemplo, la aceleración de la gravedad en la superficie terrestre no es exactamente  sino una cantidad que varía de punto a punto y cuyo valor conocido está limitado por la precisión de los aparatos experimentales empleados para medirla.
sino una cantidad que varía de punto a punto y cuyo valor conocido está limitado por la precisión de los aparatos experimentales empleados para medirla.
Por esta razón, en Ingeniería o Física no existen las cantidades con infinitos decimales, ya que esto implicaría un conocimiento perfecto de un dato experimental. Esto quiere decir que si medimos, por ejemplo, una resistencia y obtenemos un valor de aproximadamente 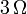 , y queremos hallar la conductancia, su valor no puede ser
, y queremos hallar la conductancia, su valor no puede ser

ya que esto significaría que conocemos todos los decimales de la inversa, aun cuando la cantidad original era solo aproximada. Un valor de

sería probablemente más correcto.
2 Cifras significativas
El primer factor que nos da información sobre la certidumbre de un dato es el número de cifras significativas. Éstas son las que, como su nombre indica, nos dan información detallada sobre el valor de la cantidad.
Como regla básica (que luego matizaremos) podemos definirlo como el número de cifras del dato, sin contar los ceros iniciales o finales. Veamos algunos ejemplos:
- 2373 Ω
- Tiene cuatro cifras significativas.
- 12.45 V
- Tiene también cuatro cifras significativas. La posición del punto decimal es irrelevante. Por ello no hay que confundir el número de cifras significativas con el número de decimales.
- 0.00987 A
- Tiene tres cifras significativas. Los ceros iniciales nos informan del orden de magnitud de la cantidad, pero no de su precisión. Esto se ve más claramente en la notación científica de un número
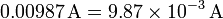
- En esta notación, cada cantidad se expresa como el producto de dos: la mantisa, formada por todas las cifras significativas, siendo mayor que 1 y menor que 10, y el exponente, que nos informa del orden de magnitud de la cantidad, que podríamos escribir como 9.87 mA
- 24.50 Ω
- Tiene cuatro cifras significativas. En este caso, el cero final es una cifra significativa, ya que si no sería superfluo. Por ello, no es lo mismo dar un resultado como 24.50 que darlo como 24.5 ya que la primera forma corresponde a una medida más precisa.
- 45000 m
- En este caso tenemos una situación ambigua, ya que el número de cifras significativas podría ser 2, 3, 4 o 5, según que los ceros finales aporten información sobre la mantisa o sólo sobre el orden de magnitud. Esta ambigüedad, de nuevo, desaparece si expresamos el número en notación científica, ya que no es lo mismo 4.5×10−4m que 4.5000×10−4m.
El último ejemplo nos muestra que la expresión normal de un número no proporciona suficiente información sobre el número de cifras significativas. Para completar esta información debemos acotar la posible incertidumbre (o error) de una cantidad.
3 Incertidumbres sistemáticas
Como primera causa de incertidumbre, que nos limita nuestros resultados, tenemos las llamadas incertidumbres sistemáticas, que se producen cuando, por algún factor externo, todas nuestras medidas resultan desviadas en el mismo sentido. En este caso, si somos capaces de identificar y medir este agente externo, podemos restar su efecto a nuestros datos.
4 Bandas de error
Más común que las incertidumbres sistemáticas, son los errores aleatorios, debidos a las imprecisiones intrínsecas del dispositivo experimental o del procedimiento de medida y que unas veces actúan en un sentido y otras en el contrario. Esta incertidumbre lleva asociada una banda de error, esto es, unos márgenes entre los cuales puede oscilar la magnitud que estamos midiendo. Si indicamos que un resultado vale
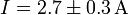
estamos diciendo que la corriente tiene una elevada probabilidad (convencionalmente se toma el 95%) de encontrarse en el intervalo entre 2.4 A y 3.0 A.
En algunas ocasiones las bandas de error pueden ser asimétricas, esto es, el límite inferior puede estar a diferente distancia del valor de la magnitud que el límite superior, indicando que tenemos la magnitud quizás mejor acotada por abajo que por arriba. Sin embargo, no es esto lo habitual. En lo que sigue nos atendremos a bandas de error simétricas en torno a su valor central.
5 Error absoluto y error relativo
Las bandas de error determinan lo que se conoce como error absoluto, E, de una cantidad, definido como la mitad de la anchura de la banda de error. Este error absoluto posee las mismas unidades que la cantidad que limita.
Una cantidad derivada de interés es el llamado error relativo de la misma cantidad, definido como

a diferencia del error absoluto, el error relativo no posee unidades, sino que se mide en tantos por uno o tantos por ciento.
Así, por ejemplo, se nos puede decir que una resistencia de 2200 Ω posee un error de ±110 Ω o que tiene una tolerancia (esto es, un error relativo) del 5%. Ambas expresiones son equivalentes. En los dos casos
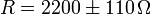
¿Cuál de los dos errores es más importante? ¿Qué debemos procurar que sea más pequeño, el error absoluto o el relativo? En lo que a información se refiere ambos proporcionan la misma ya que si conocemos uno conocemos el otro (si conocemos el valor de x, evidentemente).
En cuanto a cuál es más “importante”, depende de lo que se desee. Habrá aparatos o experimentos en los que nos interese una alta precisión (esto es, un error absoluto muy pequeño) o situaciones en las que convenga reducir el error relativo.
Como regla general, la pequeñez del error relativo es más informativa que la del error absoluto. Así, si decimos que el error al medir una masa es de 3 g, no nos dice mucho, si no sabemos cuánto vale la masa medida. No es lo mismo un error de 3 g en 1 kg que en 10 g.
Existe no obstante una excepción importante, la de aquellas medidas en que el valor de la magnitud es aproximadamente nulo. Supongamos que medimos una corriente eléctrica con una amperímetro digital de precisión 0.01 mA y resulta una medida I = 1.00±0.01 A. Esto nos da un error relativo del 1%. Supongamos que en una medida posterior de otra corriente obtenemos un resultado I = 0.00±0.01 A, con lo que ahora el error relativo es infinito, y pierde todo significado. Esto se extiende a todos los experimentos en que se busque obtener un resultado nulo. Por ejemplo, si se quiere equilibrar una balanza, lo que importa es la precisión (esto es, el error absoluto) con la que se obtiene un cero en el fiel de la balanza.





