Entrar Página Discusión Historial Go to the site toolbox

4.7. Ejemplo de movimiento de precesión

De Laplace

Contenido

1 Enunciado

El movimiento de precesión de una peonza puede describirse como una rotación en torno a un eje instantáneo que a su vez está rotando, manteniéndose fijo el punto de apoyo. Supongamos el caso particular

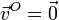
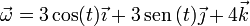
\vec{v}^O = \vec{0}        \vec{\omega}=3\cos(t)\vec{\imath}+3\,\mathrm{sen}\,(t)\vec{\jmath}+4\vec{k}
  1. Determine el campo de velocidades del sólido.
  2. Determine el campo de aceleraciones del sólido. ¿Es la aceleración de un punto igual a la derivada de la velocidad en ese punto respecto al tiempo?
  3. Halle, para cada instante las componentes intrínsecas de la aceleración y el radio de curvatura de los puntos
\overrightarrow{OA}=5\vec{k}\qquad \overrightarrow{OB}=5\vec{\imath}

2 Campo de velocidades

Por tratarse de una rotación pura

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{v}^P = \overbrace{\vec{v}^O}^{=\vec{0}} + \vec{\omega}\times\overrightarrow{OP}=\vec{\omega}\times\vec{r}= \left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k}\\ 3\cos(t) & 3\,\mathrm{sen}\,(t) & 4 \\ x & y & z\right|

Separando en componentes cartesianas

\begin{matrix} v_x & = & \omega_y z - \omega_z y & = &3z\,\mathrm{sen}\,(t)-4y\\ v_y & = & \omega_z x - \omega_x z & = &4x - 3z\cos(t)\\ v_z & = & \omega_x y - \omega_y x & = &3y\cos(t)-3x\,\mathrm{sen}\,(t) \end{matrix}

3 Campo de aceleraciones

4 Componentes intrínsecas

Obtenido de "http://tesla.us.es/wiki/index.php/4.7._Ejemplo_de_movimiento_de_precesi%C3%B3n"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace