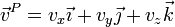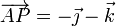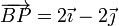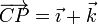4.3. Velocidad de tres puntos de un sólido

De Laplace

Revisión a fecha de 11:28 3 ago 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Valores de las constantes
3 Velocidad en P
4 Velocidad angular y de deslizamiento
5 EIRMD

1 Enunciado

Los vectores de posición y las velocidades de tres puntos de un sólido son, en el SI,

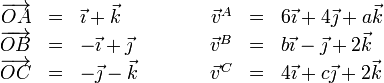
$\begin{array}{rclcrcl} \overrightarrow{OA}&=&\vec{\imath}+\vec{k}&\qquad & \vec{v}^A & = & 6\vec{\imath}+4\vec{\jmath}+a\vec{k}\\ \overrightarrow{OB}&=&-\vec{\imath}+\vec{\jmath}&\qquad & \vec{v}^B& = & b\vec{\imath}-\vec{\jmath}+2\vec{k}\\ \overrightarrow{OC}&=&-\vec{\jmath}-\vec{k}&\qquad & \vec{v}^C&=&4\vec{\imath}+c\vec{\jmath}+2\vec{k} \end{array}$

Halle los valores de $a$ , $b$ , $c$ .
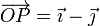Halle la velocidad del punto $\overrightarrow{OP}=\vec{\imath}-\vec{\jmath}$ .
Calcule la velocidad angular y la de deslizamiento
Determine la posición del eje instantáneo de rotación y mínimo deslizamiento.

2 Valores de las constantes

Podemos hallar las constantes indeterminadas imponiendo la condición cinemática de rigidez, esto es, la equiproyectividad del campo de velocidades:

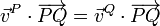
$\vec{v}^P\cdot\overrightarrow{PQ}=\vec{v}^Q\cdot\overrightarrow{PQ}$

En este caso tenemos, para los puntos A y B

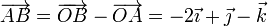
$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=-2\vec{\imath}+\vec{\jmath}-\vec{k}$

Proyectando e igualando

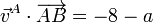
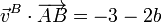
$\vec{v}^A\cdot\overrightarrow{AB}=-8-a$ $\vec{v}^B\cdot\overrightarrow{AB}=-3-2b$ $\Rightarrow$ $-a+2b=5\,$

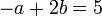
Repitiendo para A y C

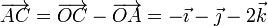
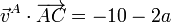
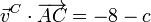
$\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}=-\vec{\imath}-\vec{\jmath}-2\vec{k}$ $\vec{v}^A\cdot\overrightarrow{AC}=-10-2a$ $\vec{v}^C\cdot\overrightarrow{AC}=-8-c$ $\Rightarrow$ $-2a+c=2\,$

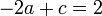
y para B y C

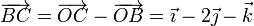
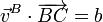
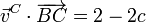
$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=\vec{\imath}-2\vec{\jmath}-\vec{k}$ $\vec{v}^B\cdot\overrightarrow{BC}=b$ $\vec{v}^C\cdot\overrightarrow{BC}=2-2c$ $\Rightarrow$ $b+2c=2\,$

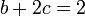
Tenemos el sistema de tres ecuaciones con tres incógnitas

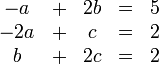
$\begin{matrix} -a&+&2b & = & 5 \\ -2a&+&c & = & 2 \\ b&+&2c & = & 2 \end{matrix}$

con solución

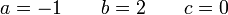
$a=-1\qquad b = 2\qquad c=0$

Las posiciones y velocidades completas de los tres puntos son entonces

$\begin{array}{rclcrcl} \overrightarrow{OA}&=&\vec{\imath}+\vec{k}&\qquad & \vec{v}^A & = & 6\vec{\imath}+4\vec{\jmath}-\vec{k}\\ \overrightarrow{OB}&=&-\vec{\imath}+\vec{\jmath}&\qquad & \vec{v}^B& = & 2\vec{\imath}-\vec{\jmath}+2\vec{k}\\ \overrightarrow{OC}&=&-\vec{\jmath}-\vec{k}&\qquad & \vec{v}^C&=&4\vec{\imath}+2\vec{k} \end{array}$

Vemos que, aunque para conocer el estado de movimiento de un sólido necesitamos las velocidades de tres de sus puntos, que en total tienen 9 componentes, solo 6 de esas componentes son necesarias, resultando las otras 3 de la condición de rigidez, como corresponde a que un sólido rígido tenga 6 grados de libertad.

3 Velocidad en P

A partir de la velocidad de tres puntos no colineales podemos determinar la velocidad angular y la de deslizamiento del sólido, y a partir de ahí la velocidad de cualquier otro punto. No obstante, también podemos hallar la velocidad de un punto a partir de la condición de rigidez. Aplicándola al formado por P y cada uno de los tres puntos conocidos, tenemos

$\vec{v}^P=v_x\vec{\imath}+v_y\vec{\jmath}+v_z\vec{k}$ $\overrightarrow{AP}=-\vec{\jmath}-\vec{k}$ $\overrightarrow{BP}=2\vec{\imath}-2\vec{\jmath}$ $\overrightarrow{CP}=\vec{\imath}+\vec{k}$

4 Velocidad angular y de deslizamiento

5 EIRMD

4.3. Velocidad de tres puntos de un sólido

De Laplace

Contenido

1 Enunciado

2 Valores de las constantes

3 Velocidad en P

4 Velocidad angular y de deslizamiento

5 EIRMD

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES