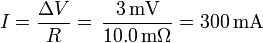Corriente y campo de un cable coaxial

De Laplace

1 Enunciado

Se tiene un cable coaxial rectilíneo de longitud L = 20 m formado por un núcleo cilíndrico de cobre de radio a = 4 mm, rodeado de una capa de dieléctrico ideal de radio exterior b = 7 mm. Por fuera del dieléctrico se encuentra una corona, también de cobre, de radio exterior c = 9 mm. El cable está terminado en un cortocircuito que conecta el núcleo interior con la corona exterior. En el extremo inicial del cable se establece una diferencia de potencial V₀ = 3 mV.

1. Calcule la intensidad de corriente que circula por el núcleo de cobre, así como la densidad de corriente y el campo eléctrico en todos los puntos del cobre.
2. Calcule el valor aproximado del campo magnético B en todos los puntos del espacio. Suponga que μ = μ₀ en todos los materiales. Desprecie los efectos de borde, considerando, para el cálculo de $\mathbf{B}$, el cable como de longitud infinita.

2 Corriente eléctrica

En este sistema tenemos dos resistencias puestas en serie. La corriente sale de la fuente de tensión y avanza por el núcleo del cable, llega al cortocircuito final y retorna por el conductor exterior, cerrándose el circuito.

Tanto en el núcleo como en la corteza exterior la corriente es longitudinal

En este caso, cada resistencia, como en el caso de un cable grueso o un tubo conductor, equivale a la de un conductor filiforme;

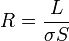
En este problema tenemos dos resistencias: la del núcleo central

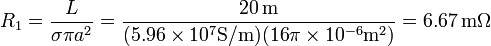
y la de la corteza exterior

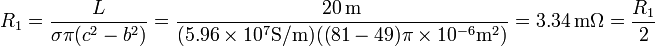
Esta resistencia es exactamente la mitad que la anterior porque en este sistema se verifica que

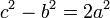
y al ser la sección de la corona el doble de la del núcleo, su resistencia es la mitad.

Puesto que están en serie, la resistencia total es la suma de ambas

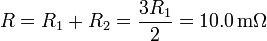
la corriente que circula por el núcleo (y retorna por la corteza) es, de acuerdo con la ley de Ohm para un circuito

3 Campo magnético