Movimiento cicloidal

De Laplace

Revisión a fecha de 19:37 27 jun 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Un punto de un disco que rueda a velocidad constante sobre una superficie plana en $y = 0$ tiene por velocidad

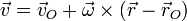
$\vec{v}=\vec{v}_O+\vec{\omega}\times\left(\vec{r}-\vec{r}_O\right)$

donde

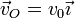
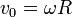
$\vec{v}_O=v_0\vec{\imath}$ $\vec{\omega}=-\omega\vec{k}$ $v_0=\omega R\,$

son la velocidad de traslación del centro del disco y la velocidad angular de rotación alrededor de él, respectivamente.

Halle la expresión de la velocidad en función de las coordenadas de un punto del disco y del tiempo.
Pruebe que las ecuaciones horarias

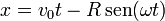
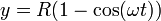
$x = v_0 t -R\,\mathrm{sen}(\omega t)$ $y = R(1-\cos(\omega t))\,$

son soluciones de las ecuaciones obtenidas en el primer apartado para un punto del borde del disco.

Para el movimiento anterior, calcule la velocidad y la aceleración instantáneas
Halle la celeridad instantánea, así como la ley horaria $s (t)$ para intervalo $0 < t < T$ con T el periodo de revolución del disco.
Determine las componentes intrínsecas de la aceleración, el radio de curvatura y la posición del centro de curvatura para el mismo periodo anterior.

2 Velocidad en función de la posición

El centro del disco avanza uniformemente, de forma que su posición en cada instante es, tomando $y = 0$ como el plano de rodadura

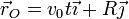
$\vec{r}_O=v_0t\vec{\imath}+R\vec{\jmath}$

La posición de un punto cualquiera del disco es

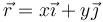
$\vec{r}=x\vec{\imath}+y\vec{\jmath}$

Sustituyendo en la expresión de la velocidad obtenemos

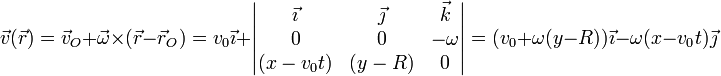
$\vec{v}(\vec{r})=\vec{v}_O+\vec{\omega}\times(\vec{r}-\vec{r}_O)=v_0\vec{\imath}+\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ 0 & 0 & -\omega \\ (x-v_0t) & (y-R) & 0\end{matrix}\right|=(v_0+\omega(y-R))\vec{\imath} - \omega(x-v_0t)\vec{\jmath}$

Si separamos en componentes obtenemos, para las derivadas respecto al tiempo de cada componente

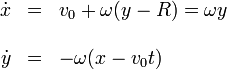
$\begin{array}{rcl}\dot{x} & = & v_0 + \omega(y-R) = \omega y \\ && \\ \dot{y} & = & -\omega(x-v_0t)\end{array}$

donde hemos aplicado que $v 0 = ω R$ .

3 Solución particular

El sistema anterior

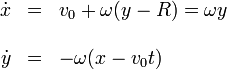
$\begin{array}{rcl}\dot{x} & = & v_0 + \omega(y-R) = \omega y \\ && \\ \dot{y} & = & -\omega(x-v_0t)\end{array}$

nos relaciona la velocidad (esto es, cómo cambia la posición con el tiempo) como función de la posición. Esto es, para determinar la posición necesitamos conocer la posición. Esta aparente circularidad (que no es tal, ya que en realidad es, para conocer la posición en $t + d t$ necesitamos conocer la posición en $t$ ) es lo que se conoce como una ecuación diferencial. Existen toda una serie de técnicas estándar para resolver este tipo de ecuaciones, pero aquí nos limitaremos a comprobar que unas determinadas ecuaciones horarias son soluciones de ellas.

Tenemos las ecuaciones horarias

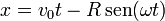
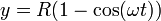
$x = v_0 t -R\,\mathrm{sen}(\omega t)$ $y = R(1-\cos(\omega t))\,$

Veamos en primer lugar que corresponden a un punto del borde del disco. Hallamos la posición relativa al centro del disco

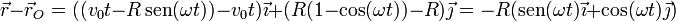
$\vec{r}-\vec{r}_O = ((v_0 t -R\,\mathrm{sen}(\omega t))-v_0t)\vec{\imath}+(R(1-\cos(\omega t))-R)\vec{\jmath}=-R(\mathrm{sen}(\omega t)\vec{\imath}+\cos(\omega t)\vec{\jmath})$

El módulo de este vector es

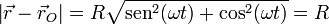
$\left|\vec{r}-\vec{r}_O\right| = R\sqrt{\mathrm{sen}^2(\omega t)+\cos^2(\omega t)} = R$

Luego efectivamente se encuentra sobre la circunferencia exterior.

Movimiento cicloidal

De Laplace

1 Enunciado

2 Velocidad en función de la posición

3 Solución particular

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES