Inmersión de un bloque metálico en agua
De Laplace
Contenido |
1 Enunciado
Un bloque de cobre de 50 kg a 80°C se deja caer en un tanque aislado adiabáticamente que contiene 120 l de agua a 25°C. Determine la temperatura final de equilibrio y la variación total del entropía.
Dato: cp(cobre) = 0.095 cal/g·°C.
2 Temperatura final
Al sumergirse, el cobre se enfría, cediendo calor al agua, que se calienta. El equilibrio se alcanza cuando ambos se ponen la misma temperatura.
La temperatura de equilibrio la obtenemos igualando el calor cedido por el cobre con el absorbido por el agua
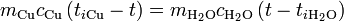
Sustituyendo
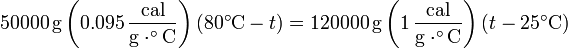
que tiene por solución
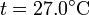
3 Variación de la entropía
3.1 Del cobre
Al enfriarse, la entropía del cobre disminuye. Si el calor específico puede suponerse independiente de la temperatura, la variación de entropía es igual a
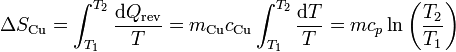
siendo su valor numérico
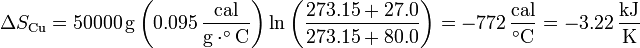
3.2 Del agua
El agua se calienta, por lo que su entropía aumenta. Suponiendo de nuevo que el calor específico puede suponerse independiente de la temperatura (lo cual es muy razonable dado que el agua se calienta menos de 2 grados), la variación de entropía es
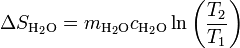
siendo su valor numérico
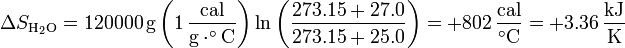
3.3 Total
Sumando los dos incrementos obtenemos la variación de entropía total
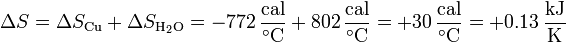
La variación neta de entropía es positiva, como corresponde a un proceso irreversible en un sistema aislado (no hay intercambio de calor con el exterior).
Hay que señalar que, aunque se calcula la entropía suponiendo un proceso reversible en el que la temperatura de los dos componentes varía gradualmente de su valor inicial al final, no es eso lo que ocurre realmente. La variación es abrupta y puede ser no uniforme (las partes del agua en contacto con el cobre se calientan antes que las alejadas). Lo que hacemos es emplear un proceso reversible que lleve del mismo estado inicial al final ya que, por tratarse la entropía de una función de estado, su incremento es independiente del camino elegido.





