Campos eléctricos y magnéticos debidos a un tubo de corriente

De Laplace

Revisión a fecha de 22:09 24 may 2010; Gabriel (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Introducción
3 Campo eléctrico,
4 Campo magnético,
5 Densidades de energía electromagnética
6 Vector de Poynting,
7 Velocidad de propagación de la energía

1 Enunciado

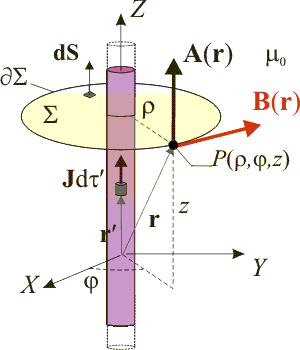
Un cilindro de radio $a$ y longitud infinita posee una densidad de carga uniforme $ρ 0$ . El cilindro se mueve con velocidad constante 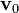$\mathbf{v}_0$ paralelamente a su eje, de forma que existe una densidad de corriente 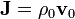$\mathbf{J} = \rho_0\mathbf{v}_0$ . Para todos los puntos del espacio halle:

El campo eléctrico, $\mathbf{E}$ .
El campo magnético, $\mathbf{B}$ .
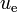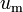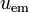Las densidades de energía eléctrica, $u_\mathrm{e}\,$ , magnética, $u_\mathrm{m}\,$ y electromagnética, $u_\mathrm{em}\,$ .
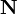El vector de Poynting, $\mathbf{N}$ .
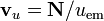La velocidad de propagación de la energía, definida como $\mathbf{v}_u=\mathbf{N}/u_\mathrm{em}$ .

2 Introducción

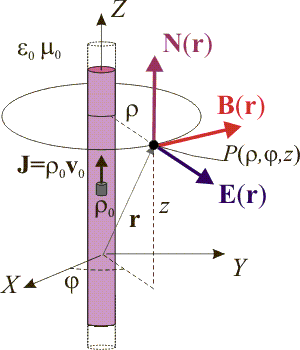
Respecto de un sistema de referencia fijo, el cilindro infinito de radio

a

cargado uniformemente con una densidad de carga eléctrica

ρ 0

, constituye una corriente eléctrica cuando se mueve con una velocidad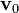 $\mathbf{v}_0$ . Tomando el sistema de referencia con el eje

Z

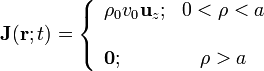
colienal con el eje del cilindro y utilizando las coordenadas cilíndricas $(\rho,\varphi,z)$ , dicha corriente eléctrica estará caracterizada por la densidad volumétrica, $\mathbf{J}(\mathbf{r}; t)=\left\{\begin{array}{lc}\rho_0v_0\mathbf{u}_z; & 0<\rho <a \\ \\ \mathbf{0}; & \rho>a \end{array}\right.$

Como la densidad de carga eléctrica en cada punto de la distribución permanece constante, la corriente que genera su movimiento es estacionaria. Y como tampoco varía en el tiempo, será fuente de un campo magnetostático.

Pero además, consideremos un diferencial fijo de volumen $dτ$ situado en el entorno de un punto $P$ con $ρ < a$ . Como se halla dentro de la región ocupada por la distribución cilíndrica de carga, en cada instante de tiempo existirá en $Δτ$ una cierta cantidad de carga. Obsérvese que ésta permanecerá constante en el tiempo ya que, aunque la carga se está moviendo, las cantidades de carga que entran y salen en $Δτ$ en un diferencial de tiempo son idénticas. Nótese que para que esto ocurra es necesario que la distribución de carga en el cilíndro móvil sea uniforme.

En consecuencia, un observador ligado al sistema de refencia fijo observará en todo momento una distribución estacionaria de carga que será fuente de un campo eléctrostático 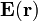$\mathbf{E}(\mathbf{r})$ . Dicha distribución está descrita en todo el espacio por la función volumétrica de carga,

$\rho_e(\mathbf{r}; t)=\left\{\begin{array}{lc}\rho_0; & 0<\rho <a \\ \\ 0; & \rho>a \end{array}\right.$

3 Campo eléctrico, $\mathbf{E}$

Como se discutió anteriormente, la corriente eléctrica generará un campo magnetostático, por lo que el campo eléctrico existente se deberá exclusivamente a la distribución estática de carga eléctrica que acabamos de describir. Dicho campo es irrotacional y deriva de un potencial electrostático $\phi(\mathbf{r})=\phi(\rho,\varphi,z)$ , en general. Pero dada la simetría cilíndrica de la distribución y su longitud infinita, podemos asegurar que el valor del potencial en un punto sólo va a depender de la distancia $ρ$ al eje $Z$ (eje de la districión de carga), lo que lleva a que el campo eléctrico también va a presentar simetría cilíndrica:

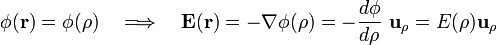
$\phi(\mathbf{r})=\phi(\rho) \quad \Longrightarrow \quad\mathbf{E(r)}=-\nabla \phi(\rho)=-\frac{d\phi}{d\rho}\ \mathbf{u}_\rho=E(\rho) \mathbf{u}_\rho$

A partir de este resultado es fácil determinar la expresión de la intensidad del campo eléctrico mediante la Ley de Gauss. Para ello, consideraremos un recinto cilíndrico $Δτ$ , colineal con la distribución de carga y con radio y altura arbitrarios, $ρ$ y $Δ z$ , respectivamente. El flujo del campo eléctrico a través de la superficie cerrada 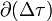$\partial\big(\Delta\tau\big)$ que limita dicho volumen es proporcional a la cantidad de carga eléctrica $Δ Q$ contenida en él. Para una altura $Δ z$ fija, $Δ Q$ va a ser la misma siempre que el radio $ρ$ del volumen $Δτ$ sea mayor que el radio $a$ de la distribución de carga. Sin embargo, si $ρ < a$ , la cantidad de carga contenida es proporcional a cuadrado del radio de $Δτ$ :

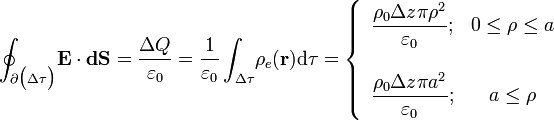
$\oint_{\partial\big(\Delta\tau\big)}\!\mathbf{E\cdot dS}=\frac{\Delta Q}{\varepsilon_0}=\frac{1}{\varepsilon_0}\int_{\Delta\tau}\!\rho_e(\mathbf{r})\mathrm{d}\tau=\left\{ \begin{array}{lc}\displaystyle \frac{\rho_0\Delta z\pi\rho^2}{\varepsilon_0};&0\leq\rho\leq a \\ \\ \displaystyle\frac{\rho_0\Delta z\pi a^2}{\varepsilon_0};& a\leq\rho\end{array}\right.$

Por otra parte, puesto que el campo eléctrico tiene la dirección de 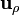$\mathbf{u}_\rho$ en todos los puntos, sólo existirá flujo no nulo a través de la superficie lateral de 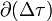$\partial\big(\Delta\tau\big)$ . Igualando el resultado de este cálculo con el anteriormente obtenido para la carga, se determina la expresión del campo eléctrico en todo el espacio:

$\oint_{\partial\big(\Delta\tau\big)}\!\mathbf{E\cdot dS}=\int_0^{2\pi}\!\mathrm{d}\varphi \int_0^{\Delta z}\!E(\rho)\rho\mathrm{d}z=2\pi \Delta z\ \rho\ E(\rho)$ $\Rightarrow$ $\mathbf{E(r)}=E(\rho) \mathbf{u}_\rho=\left\{ \begin{array}{lc}\displaystyle \frac{\rho_0}{2\varepsilon_0}\ \rho\ \mathbf{u}_\rho;&0\leq\rho\leq a \\ \\ \displaystyle \frac{\rho_0a^2}{2\varepsilon_0\rho}\ \mathbf{u}_\rho ;& a\leq\rho\end{array}\right.$

4 Campo magnético, $\mathbf{B}$

En el sistema bajo estudio no existen materiales con propiedades magnéticas, por tanto, la corriente eléctrica estacionaria y constante producida por el movimiento del cilindro cargado es la única fuente del campo de inducción mangética 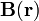$\mathbf{B}(\mathbf{r})$ . Como es bien sabido, una propiedad fundamental de éste es su carácter solenoidal, por lo que deriva de un potencial vector 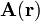$\mathbf{A}(\mathbf{r})$ que depende directamente de las fuentes del campo magnético; en el caso que nos ocupa se tendrá:

$\mathbf{A}(\mathbf{r})= \frac{\mu_0}{4\pi}\ \int_{\mathrm{I\!R}^3} \!\frac{\mathbf{J(r')}\ \mathrm{d}\tau'}{|\mathbf{r}-\mathbf{r}'|}=\mathbf{u}_z \ \frac{\mu_0 \rho_0v_0}{4\pi}\ \int_{\rho<a}\!\frac{\mathrm{d}\tau'}{|\mathbf{r}-\mathbf{r}'|}=A(\rho)\mathbf{u}_z$

No hace falta calcular esta integral pues nos basta con saber que el potencial vector en cualquier punto sólo va a tener componente en la dirección paralela al eje de la distribución. Además, debido a la geometría cilíndrica de la distribución de corriente y su longitud infinita, el valor de dicha componente en un punto arbitrario sólo dependerá de la distancia $ρ$ que lo separa del eje $Z$ . A partir de este resultado es fácil determinar la geometría del campo 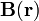$\mathbf{B}(\mathbf{r})$ ,

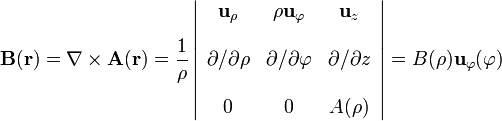
$\mathbf{B}(\mathbf{r})=\nabla\times\mathbf{A}(\mathbf{r})=\frac{1}{\rho}\left|\begin{array} {ccc}\mathbf{u}_{\rho} & \rho \mathbf{u}_{\varphi} & \mathbf{u}_z \\ \\ \partial/\partial\rho & \partial/\partial\varphi & \partial/\partial z \\ \\ 0 & 0 & A(\rho) \end{array}\right|=B(\rho)\mathbf{u}_\varphi(\varphi)$

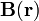así como su expresión en todo el espacio, mediante la aplicación de la Ley de Ampère. Tomemos una circunferencia $\partial\Sigma$ de radio arbitrario $ρ$ , centrada en un punto cualquiera del eje $Z$ y contenida en un plano perpendicular a dicho eje. La Ley de Ampère establece que la circulación del campo $\mathbf{B}(\mathbf{r})$ sobre una curva cerrada $\partial\Sigma$ es proporcional a la intensidad de corriente que atraviesa cualquier superficie que se apoye en dicha curva; por ejemplo, el disco $Σ$ de radio $ρ$ . 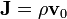En el caso que nos ocupa, dicha intensidad es el flujo de la densidad $\mathbf{J}=\rho\mathbf{v}_0$ a través de $Σ$ , que tendrá el mismo valor $I 0$ siempre que el disco sea mayor que la sección transversal del tubo de carga en movimiento, y que será función de $ρ$ cuando el valor de este parámetro sea menor que $a$ :

$\int_{\partial\Sigma}\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge\mathbf{B}\cdot\mathrm{d}\mathbf{r}=\mu_0\int_\Sigma\!\mathbf{J(r)}\cdot\mathrm{d}\mathbf{S}=\left\{\begin{array}{lc}\mu_0\rho_0v_0\pi\rho^2;& 0\leq \rho\leq a\\ \\ \mu_0\rho_0v_0\pi a^2=\mu_0I_0; & a\leq \rho\end{array}\right.$

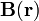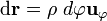Por otra parte, calculamos la circulación del campo $\mathbf{B}(\mathbf{r})$ sobre la curva $\partial\Sigma$ teniendo en cuenta la forma del campo y que el vector elemento de arco sobre la curva es $\mathrm{d}\mathbf{r}=\rho\ d\varphi\mathbf{u}_\varphi$ . Exigiendo que esta circulación debe ser igual a la corriente antes calculada, se obtiene la expresión del campo de inducción magnética:

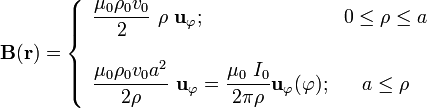
$\int_{\partial\Sigma}\!\!\!\!\!\!\!\!\!\!\bigcirc\!\!\!\!\wedge\mathbf{B}\cdot\mathrm{d}\mathbf{r}=2\pi \rho B(\rho)$ $\Rightarrow$ $\mathbf{B}(\mathbf{r})=\left\{\begin{array}{lc}\displaystyle\frac{\mu_0\rho_0v_0}{2}\ \rho\ \mathbf{u}_\varphi; & 0\leq \rho\leq a \\ \\ \displaystyle \frac{\mu_0\rho_0v_0 a^2}{2\rho}\ \mathbf{u}_\varphi =\frac{\mu_0\ I_0}{2\pi\rho}\mathbf{u}_\varphi(\varphi); & a\leq \rho\end{array}\right.$

5 Densidades de energía electromagnética

En el sistema bajo estudio se considera una total ausencia de medios materiales: el cilindro de corriente y carga consiste en una distribución continua de carga eléctrica que se mueve en el vacío. Los presencia de campos eléctrico y magnético estáticos generados por dicha distribución implican la existencia de sendas formas energías eléctrica y magnética en dicho espacio, que permancerán invariantes en el tiempo. La cantidad por unidad de volumen (densidad) de estas energías en cada punto pueden ser calculadas de forma sencilla mediante las siguientes expresiones:

$u_\mathrm{e}\mathbf(r)=\frac{\varepsilon_0}{2}|\mathbf{E(r)}|^2=\left\{ \begin{array}{lc}\displaystyle \frac{\rho_0^2}{8\varepsilon_0}\ \rho^2;&0\leq\rho\leq a \\ \\ \displaystyle \frac{\rho_0^2}{8\varepsilon_0}\left(\frac{a^2}{\rho}\right)^2; & a\leq\rho\end{array}\right.$ $\qquad$

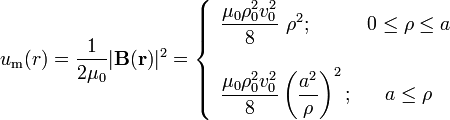
$u_\mathrm{m}\mathbf(r)=\frac{1}{2\mu_0}|\mathbf{B(r)}|^2=\left\{\begin{array}{lc}\displaystyle\frac{\mu_0\rho_0^2v_0^2}{8}\ \rho^2; & 0\leq \rho\leq a \\ \\ \displaystyle \frac{\mu_0\rho_0^2v_0^2}{8}\left(\frac{a^2}{\rho}\right)^2 ; & a\leq \rho\end{array}\right.$

La distribución de energía electromagnética en el espacio está descrita por la suma en cada punto de las densidades de energía eléctrica y magnética:

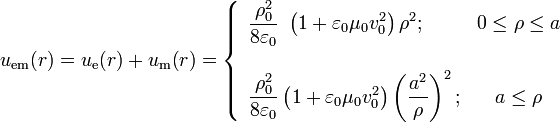
$u_\mathrm{em}\mathbf(r)=u_\mathrm{e}\mathbf(r)+u_\mathrm{m}\mathbf(r)=\left\{ \begin{array}{lc}\displaystyle \frac{\rho_0^2}{8\varepsilon_0}\ \left(1+\varepsilon_0\mu_0v_0^2\right) \rho^2;&0\leq\rho\leq a \\ \\ \displaystyle \frac{\rho_0^2}{8\varepsilon_0}\left(1+\varepsilon_0\mu_0v_0^2\right)\left(\frac{a^2}{\rho}\right)^2; & a\leq\rho\end{array}\right.$

6 Vector de Poynting, 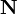$\mathbf{N}$

El vector de Poynting se utiliza para describir los procesos de propagación de la energía electromagnética. Concretamente, la proyección de este vector en una determinada dirección indica la cantidad de energía electromagnética que por unidad de tiempo y superficie se propaga en dicha dirección. Para el caso de campos eléctrico y magnético en el vacío, como el que nos ocupa, se tiene:

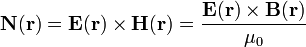
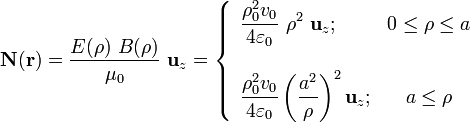
$\mathbf{N(r)}=\mathbf{E(r)}\times\mathbf{H(r)}=\frac{\mathbf{E(r)}\times\mathbf{B(r)}}{\mu_0}$ $\Rightarrow$ $\mathbf{N(r)}=\frac{E(\rho)\ B(\rho)}{\mu_0}\ \mathbf{u}_z=\left\{ \begin{array}{lc}\displaystyle \frac{\rho_0^2v_0}{4\varepsilon_0} \ \rho^2 \ \mathbf{u}_z;&0\leq\rho\leq a \\ \\ \displaystyle \frac{\rho_0^2v_0}{4\varepsilon_0}\left(\frac{a^2}{\rho}\right)^2 \mathbf{u}_z ;& a\leq\rho\end{array}\right.$

Es decir, a pesar de que el cilindro cargado en movimiento genera sendos campos estáticos, existe un flujo constante de energía electromagnética que tiene su valor máximo en la dirección en que se mueve el cilindro. Este hecho puede entenderse fácilmente sin más que evaluar el Teorema de Poyting en un volumen fijo arbitrario

Δτ

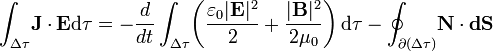
: $\int_{\Delta\tau}\!\mathbf{J\cdot E}\mathrm{d}\tau=-\frac{d}{dt}\int_{\Delta\tau}\!\left(\frac{\varepsilon_0|\mathbf{E}|^2}{2}+\frac{|\mathbf{B}|^2}{2\mu_0}\right)\mathrm{d}\tau-\oint_{\partial(\Delta\tau)}\!\mathbf{N}\cdot\mathbf{dS}$

El primer miembro de la expresión anterior es nulo cualquiera que sea $Δτ$ , pues aunque el campo eléctrico existe en todo el espacio, la densidad de corriente sólo es distinta de cero dentro del cilindro cargado y en esta región $\mathbf{J}\perp\mathbf{E}$ . El primer término del segundo miembro es también nulo, pues la densidad de energía electromagnética en cualquier punto es invariante en el tiempo; por tanto, la energía total almacenada en cualquier volumen finito también permanece invariante y su derivada temporal es nula. En consecuencia, el flujo neto del vector de Poynting a través de cualquier superficie cerrada $\partial(\Delta\tau)$ va a ser nulo: es decir, en todo instante las cantidades de energía electromagnética que entran y salen en cualquier recinto $Δτ$ son idénticas.

7 Velocidad de propagación de la energía

El cociente entre el módulo del vector de Poynting y la densidad de energía tiene dimensiones de espacio partido de tiempo. Por tanto, dividiendo el vector de Poynting por el valor de la densidad de energía electromagnética en cada punto se define un campo vectorial que describe cómo es la velocidad de propagación de la energía. En el sistema bajo estudio se obtiene,

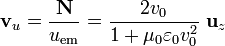
$\mathbf{v}_u=\frac{\mathbf{N}}{u_\mathrm{em}}=\frac{2v_0}{1+\mu_0\varepsilon_0v_0^2}\ \mathbf{u}_z$

Es decir, dicho campo de velocidades es uniforme, o lo que es lo mismo, la energía electromagnética se propaga con la mimsa velocidad, dirección y sentido en todos los puntos del espacio. Teniendo en cuenta que 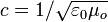$c=1/\sqrt{\varepsilon_0\mu_o}$ es la constante universal correspondiente a la velocidad de propagación de la luz en el vacío, se obtiene que la velocidad de propagación de la energía electromagnética en el sistema bajo estuido es:

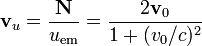
$\mathbf{v}_u=\frac{\mathbf{N}}{u_\mathrm{em}}=\frac{2\mathbf{v}_0}{1+(v_0/c)^2}$

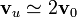Según esta expresión se obtiene que cuando la velocidad del cilindro es muy pequeña comparada con la de la luz ( $v_0\ll c$ ), la velocidad de propagación de la energía es prácticamente el doble que la del movimiento del cilindro: $\mathbf{v}_u\simeq 2\mathbf{v}_0$ . Conforme la velocidad del cilindro aumenta, la velocidad de propagación de la energía disminuye, tendiendo a igualarse a la del movimiento del cilindro conforme ésta se aproxima al valor $c$ de la velocidad de la luz.

Campos eléctricos y magnéticos debidos a un tubo de corriente

De Laplace

Contenido

1 Enunciado

2 Introducción

3 Campo eléctrico, $\mathbf{E}$

4 Campo magnético, $\mathbf{B}$

5 Densidades de energía electromagnética

6 Vector de Poynting, $\mathbf{N}$

7 Velocidad de propagación de la energía

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES