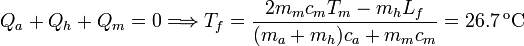Mezcla de agua y hielo con bloque metálico
De Laplace
Contenido |
1 Enunciado
Un calorímetro contiene 500 g de agua y 300 g de hielo, todo ello a una temperatura de 0oC. Se coge un bloque metálico de 1000 g de un horno cuya temperatura es de 240oC y se deja caer rápidamente dentro del calorímetro, resultando que se produce exactamente la fusión de todo el hielo. ¿Cuál sería la temperatura final del sistema si la masa de hierro fuese el doble? Desprecia las pérdidas caloríficas del calorímetro y su capacidad calorífica.
2 Solución
2.1 Fusión del hielo
En este primer proceso se nos dice que el único efecto de dejar caer el bloque metálico en el calorímetro es fundir todo el hielo. La mezcla de agua y hielo estaba a 0oC inicialmente. Durante el cambio de fase de hielo a agua líquida la temperatura no cambia, por lo que la temperatura final del agua y el hielo es la misma que la inicial, Ta = 0oC.
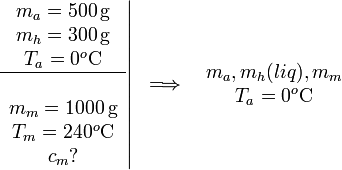
La incógnita es cm, el calor específico del metal.
Veamos el calor absorbido por cada sistema
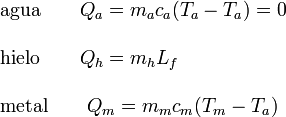
Como el sistema completo es cerrado, la suma de calores transferidos internamente es cero.
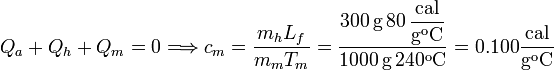
2.2 Añadido de una masa doble
En este caso, además de fundirse el hielo la temperatura final es mayor que 0oC, pues el trozo de metal puede transferir más calor que antes. Podemos describir la evolución como
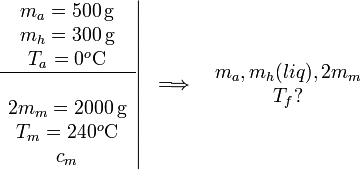
La incógnita es Tf, la temperatura final del sistema.
Veamos el calor absorbido por cada sistema
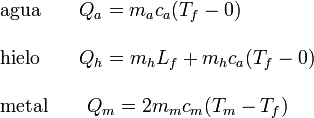
De nuevo, la suma de calores transferidos internamente es cero