Generador

De Laplace

1 Introducción

2 Definición de generador

3 Definición de fuerza electromotriz

La acción neta de las fuerzas no electrostáticas que actúan en los generadores se mide con la fuerza electromotriz, cuya unidad es el voltio y definida como

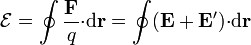
esto es, la integral a lo largo de una curva cerrada de la fuerza total por unidad de carga. Esta fuerza total incluye al campo electrostático como al campo efectivo .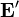

En circuito abierto, la fuerza electromotriz equivale a la diferencia de potencial entre bornes del generador

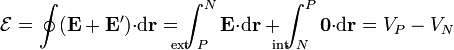
Cuando se establece la corriente, el campo no electrostático no sólo debe compensar al campo eléctrico, sino que debe devolver a las cargas, que han circulado por el exterior, a su electrodo original. Por ello, debe ser superior al campo eléctrico, ya que ha de superar la resistencia que opone el propio generador al movimiento de cargas por su interior, lo que se expresa a través de la relación

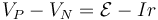
donde V_P − V_N es la diferencia de potencial entre bornes, I la corriente que atraviesa el generador y r la resistencia interna de éste.

Hay que remarcar que en el interior de un generador no se verifica la ley de Ohm, ya que la corriente o bien es nula o bien va en sentido opuesto al campo eléctrico. En todo caso, se verifica 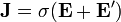cuando el agente externo actúa en un medio óhmico.

Modelando un generador real en un circuito equivalente, lo podemos considerar como compuesto de un generador ideal (sin resistencia interna) asociado en serie con una resistencia r.

Cuando se describe una curva cerrada en un sistema en estado estacionario, atravesando uno o varios generadores, la definición de fuerza electromotriz, trasladada al circuito equivalente, conduce a la ley de Kirchhoff para las mallas

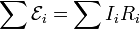
donde las I_i son las corrientes que circulan por las distintas ramas que recorremos, y las R_i incluyen también las resistencias internas de las fuentes.

4 Relación con el voltaje

4.1 En circuito abierto

4.2 En circuito cerrado

5 Potencia de un generador

6 Modelo circuital de generador

6.1 Fuente de tensión

6.2 Fuente de intensidad

7 Ejemplos

7.1 Generador de Van de Graaf

7.2 Espira móvil