Incertidumbre de varias medidas de la misma magnitud

De Laplace

Revisión a fecha de 16:42 18 mar 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Valor de la medida
3 Estimación de la incertidumbre
- 3.1 Expresión relativa a la media y error de redondeo
4 Caso de una magnitud función de otra(s)

1 Introducción

En muchos casos, una sola medida de una cantidad no nos da suficiente información sobre el error de una magnitud. Puede ocurrir que hagamos una medida única, con un error de medida muy pequeño, pero, por la propia naturaleza del experimento o del dispositivo de medida, sepamos que ese resultado puede haberse desviado del valor “real” de la cantidad, esto es, que haya una incertidumbre intrínseca, no achacable a la imprecisión del aparato de medida. En este caso, obtendremos una mejor aproximación efectuando una serie de medidas sucesivas y elaborando un estudio estadístico, que nos dirá como se distribuyen los resultados. También puede ocurrir que hayamos obtenido diferentes valores de la misma magnitud por procedimientos diferentes y queramos combinar los resultados en uno solo.

2 Valor de la medida

Si tenemos $n$ valores, $x i$ , de la misma magnitud $x$ , que se supone que representan al mismo valor real y que han sido medidos independientemente (esto es, que el hecho de realizar una de las medidas no afecta a los resultados de las demás medidas), tomaremos como estimación de la cantidad $x$ la media aritmética de las distintas medidas

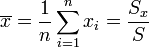
$\overline{x}=\frac{1}{n}\sum_{i=1}^n x_i = \frac{S_x}{S}$

donde hemos definido las cantidades $S$ y $S x$ (que luego usaremos más ampliamente) como

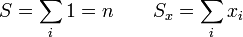
$S = \sum_i 1 = n \qquad S_x = \sum_i x_i$

(en los sumatorios sobre $i$ se entenderá siempre que se extiende desde $1$ hasta $n$ , el número de datos).

Ejemplo: Supongamos que las sucesivas medidas de una distancia hechas con una regla de precisión 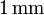$1\,\mathrm{mm}$ , nos dan

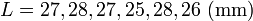
$L = 27, 28, 27, 25, 28, 26\ (\mathrm{mm})$

teniendo cada valor un error individual de 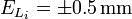$E_{L_i}= \pm 0.5\,\mathrm{mm}$ . En este caso asignaremos como valor medido de la corriente

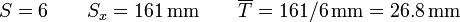
$S= 6 \qquad S_x = 161\,\mathrm{mm}\qquad \overline{T}= 161/6 \,\mathrm{mm} = 26.8\,\mathrm{mm}$

El cálculo exacto daría 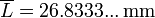$\overline{L}=26.8333...\,\mathrm{mm}$ . A la hora de expresar el resultado final no se puede dar con más decimales que los que permite la precisión. Sin embargo, para los cálculos intermedios, como los del error que veremos ahora, es conveniente anotar este valor con más decimales (dos o tres más, como mínimo).

3 Estimación de la incertidumbre

Asignaremos como incertidumbre (o error) de la cantidad $x$ el doble de la desviación cuadrática media de la media de los datos, estimado como

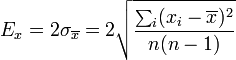
$E_x = 2\sigma_{\overline{x}} = 2\sqrt{\frac{\sum_i(x_i-\overline{x})^2}{n(n-1)}}$

La justificación de esta fórmula se indica en otro artículo

Esta cantidad no viene implementada directamente en las calculadoras u hojas de cálculo (como \emph{Excel}), pero es inmediata a partir de la llamada desviación estándar de la muestra, $σ n - 1$ (en las calculadoras $x σ n - 1$ ) o de la llamada desviación estándar de la población, $σ n$ (en las calculadoras $x σ n$ ), que sí aparecen. Estas dos funciones están definidas como

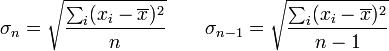
$\sigma_n = \sqrt{\frac{\sum_i(x_i-\overline{x})^2}{n}}\qquad \sigma_{n-1} = \sqrt{\frac{\sum_i(x_i-\overline{x})^2}{n-1}}$

de forma que el error puede calcularse a partir de cualquiera de ellas como

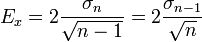
$E_x = 2\frac{\sigma_n}{\sqrt{n-1}} = 2\frac{\sigma_{n-1}}{\sqrt{n}}$

Caso de que no estén disponibles, el error, puede hallarse a partir de los sumatorios, ya que al desarrollar tenemos

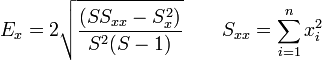
$E_x = 2\sqrt{\frac{(SS_{xx}-S_x^2)}{S^2(S-1)}}\qquad S_{xx}=\sum_{i=1}^n x_i^2$

Ejemplo: Para los mismas medidas de la longitud

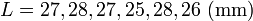
$L = 27, 28, 27, 25, 28, 26\ (\mathrm{mm})$

el cálculo del error seguiría los siguientes pasos (que la calculadora hace directamente)

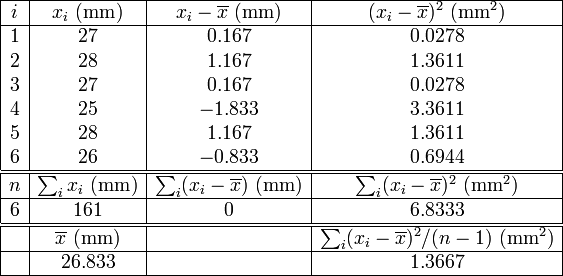
$\begin{array}{|c|c|c|c|} \hline i & x_i\ (\mathrm{mm}) & x_i-\overline{x}\ (\mathrm{mm}) & (x_i-\overline{x})^2\ (\mathrm{mm}^2)\\\hline 1 & 27 & 0.167 & 0.0278 \\ 2 & 28 & 1.167 & 1.3611 \\ 3 & 27 & 0.167 & 0.0278 \\ 4 & 25 & -1.833 & 3.3611 \\ 5 & 28 & 1.167 & 1.3611 \\ 6 & 26 & -0.833 & 0.6944 \\ \hline\hline n & \sum_i x_i\ (\mathrm{mm}) & \sum_i(x_i-\overline{x})\ (\mathrm{mm}) & \sum_i(x_i-\overline{x})^2\ (\mathrm{mm}^2)\\\hline 6 & 161 & 0 & 6.8333 \\ \hline \hline & \overline{x}\ (\mathrm{mm}) & & \sum_i(x_i-\overline{x})^2/(n-1)\ (\mathrm{mm}^2)\\ \hline & 26.833 & & 1.3667 \\\hline \end{array}$

por lo que la desviación de la muestra sería

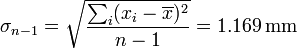
$\sigma_{n-1}= \sqrt{\frac{\sum_i(x_i-\overline{x})^2}{n-1}} = 1.169\,\mathrm{mm}$

y la estimación del error de la media

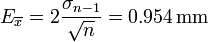
$E_{\overline{x}} = 2\frac{\sigma_{n-1}}{\sqrt{n}}= 0.954 \,\mathrm{mm}$

que redondeado nos da, para el resultado final

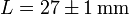
$L = 27\pm 1 \,\mathrm{mm}$

Esta estimación para el error no puede resultar inferior a la precisión del aparato de medida. Supongamos que medimos la longitud de una mesa con una regla graduada en centímetros. Lo hacemos 10 veces y en todos los casos nos resulta $L = 123.0\pm 0.5\,\mathrm{cm}$. No podemos concluir que el error es nulo (que es lo que daría la expresión anterior), sino que carecemos de la precisión suficiente para determinarlo.

Por ello, adoptaremos el siguiente criterio, si hacemos $n$ medidas, cada una de ellas con el mismo error 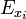$E_{x_i}$ (según se ve en el caso de una sola medida) y el error estadístico, definido anteriormente, nos da una cantidad $E est$ , tomaremos como error de la cantidad $x$ a la mayor de estas dos cantidades, esto es

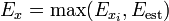
$E_x = \mbox{max}(E_{x_i},E_\mathrm{est})$

Con este error, la cantidad $x$ se indicará, convenientemente redondeada, como

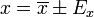
$x = \overline{x}\pm E_x$

3.1 Expresión relativa a la media y error de redondeo

Una forma más compacta de escribir la expresión del error es introduciendo las variables relativas a la media, que definimos como

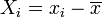
$X_i = x_i - \overline{x}$

de forma que el error queda como

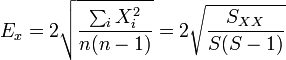
$E_x = 2 \sqrt{\frac{\sum_i X_i^2}{n(n-1)}} = 2\sqrt{\frac{S_{XX}}{S(S-1)}}$

Si es necesario calcular explícitamente esta cantidad (porque no se dispone de la función $x σ n - 1$ ) es preferible emplear la expresión con las variables relativas a la media, ya que presentan un menor error de redondeo.

Este error numérico se da cuando debemos restar dos cantidades muy próximas entre sí. Por ejemplo, supongamos que tenemos la siguiente lista de valores de una temperatura

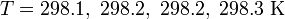
$T = 298.1,\ 298.2,\ 298.2,\ 298.3\ \mathrm{K}$

y tratamos de hallar la media y el error de esta temperatura.

La media de estos valores nos da

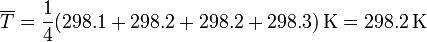
$\overline{T} = \frac{1}{4}(298.1+298.2+298.2+298.3)\,\mathrm{K} = 298.2\,\mathrm{K}$

y para el error tenemos, en primer lugar, que

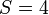
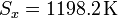
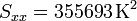
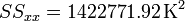
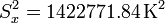
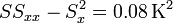
$S = 4\,$ $S_x = 1198.2\,\mathrm{K}$ $S_{xx}= 355693\,\mathrm{K}^2$ $SS_{xx} = 1422771.92 \,\mathrm{K^2}$ $S_x^2 = 1422771.84\,\mathrm{K^2}$ $SS_{xx}-S_x^2 = 0.08\,\mathrm{K}^2$

y resulta el error

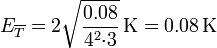
$E_{\overline{T}} = 2\sqrt{\frac{0.08}{4^2{\cdot}3}} \,\mathrm{K} = 0.08\,\mathrm{K}$

Vemos que a la hora de calcular el error podemos tener problemas al hacer la resta de dos números grandes como $S S x x$ y 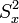$S_x^2$ ya que si la calculadora retiene solo 7 cifras perdemos los dos últimos y nos resulta (erróneamente) un error nulo.

Por ello, desde el punto de vista numérico es preferible emplear la cantidades relativas a la media, con las que el cálculo quedaría como

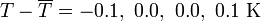
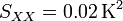
$T -\overline{T}= -0.1,\ 0.0,\ 0.0,\ 0.1\ \mathrm{K}$ $S_{XX} = 0.02\,\mathrm{K}^2$

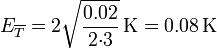
$E_{\overline{T}} = 2\sqrt{\frac{0.02}{2{\cdot}3}}\,\mathrm{K} = 0.08\,\mathrm{K}$

En este caso no tenemos que preocuparnos de $S X$ (que es siempre nulo) ni de los errores de redondeo (aunque estos pueden aparecer al hallar 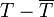$T-\overline{T}$ , esta situación se da en muy pocos casos).

4 Caso de una magnitud función de otra(s)

En los dos apartados anteriores hemos visto cómo obtener y expresar una cantidad sujeta a error a partir de las medidas directas de dicha magnitud.

En muchos casos, no obstante, debemos trabajar con cantidades indirectas, obtenidas a partir de las medidas. Estas pueden depender de una sola variable experimental $z = f (x)$ o de varias magnitudes diferentes 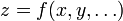$z = f(x,y,\dots)$ .

Incertidumbre de varias medidas de la misma magnitud

De Laplace

Contenido

1 Introducción

2 Valor de la medida

3 Estimación de la incertidumbre

3.1 Expresión relativa a la media y error de redondeo

4 Caso de una magnitud función de otra(s)

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES