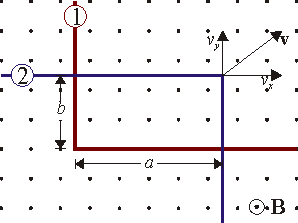
Conductor que se desplaza sobre otro
De Laplace
Contenido |
1 Enunciado
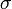y sección 
. Uno de los conductores ("1") es fijo, mientras que el segundo ("2") puede deslizarse manteniendo el contacto con el primero y su orientación, de forma que entre ambos conductores definen un rectángulo de base 
y altura . El conductor móvil se desplaza con velocidad constante, de forma que
Todo el sistema está sometido a un campo magnético no uniforme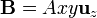 
, perpendicular al plano de los conductores.
- Calcule la corriente que circula por el sistema en cada instante. Desprecie el efecto de la autoinducción.
- Halle la fuerza que se ejerce sobre el conductor móvil.
2 Solución
2.1 Cálculo de la corriente
La corriente la obtenemos por aplicación de la ley de Faraday en forma integral \[ IR = -\dtot{\Phi_m}{t} \] siendo $\Phi_m$ el flujo magnético a través de una superficie apoyada en la espira.
\dibujops{flujo2} La espira está definida por el rectángulo de lados $x$ e $y$, ya que la corriente fluye por sus cuatro lados, pasando de una varilla a la otra en los puntos de contacto. Por los tramos restantes de ambas varillas no circula corriente, por estar abiertas.
Recorremos esta espira en sentido antihorario de forma que la normal vaya en la dirección y sentido de $\mathbf{u}_{z}$, que es el sentido del campo. De este modo el flujo es una cantidad positiva.
Al ser el campo magnético uniforme, el flujo es \[ \Phi_m = \int \mathbf{B}{\cdot}\mathrm{d}\mathbf{S} = B_0 x y = B_0\left(x_0+ v_x t\right)\left(y_0 + v_yt\right) \] La fuerza electromotriz en el circuito es la derivada de esta cantidad, cambiada de signo: \[ \mathcal{E} = -\dtot{\Phi_m}{t}= -B_0\left(v_x(y_0+v_yt)+v_y(x+v_0t)\right) = -B_0\left(x_0v_y+y_0v_x +2v_xv_yt\right) \] Esta fuerza electromotriz es igual a $IR$ donde $R$ es la resistencia de la espira. Esta resistencia cambia en el tiempo, ya que las dimensiones de la espira se van modificando. Será igual a \[ R(t) = \frac{l}{\sigma A} = \frac{2(x+y)}{\sigma A} \] siendo $A$ la sección del hilo y $\sigma$ su conductividad. $l=2(x+y)$ es el perímetro del rectángulo.
Sustituyendo obtenemos la corriente \[ I=\frac{\mathcal{E}}{R} = -\frac{\sigma A B_0\left(x_0v_y+y_0v_x +2v_xv_yt\right)}{2(x_0+y_0+(v_x+v_y)t)} \] El sentido asignado a esta corriente, tal como se indicó antes, es antihorario. Dependiendo del signo de $I$ (que a su vez depende de hacia dónde se mueve la varilla) el sentido real de la corriente será el supuesto o el opuesto.
2.2 Cálculo de la fuerza
\casol En este caso, aplicando la misma técnica tenemos que el flujo es \[ \Phi_m = B_0 x y = B_0 \left(R \ee^{\alpha t}\right)\left(R\ee^{-\alpha t}\right)= B_0R^2 \] pero esta cantidad es una constante, ya que aunque varían las dos dimensiones, el área del rectángulo permanece fija (su vértice se mueve sobre la hipérbola $xy=R^2$). Por tanto, \[ \mathcal{E} = -\dtot{\Phi_m}{t}=0 \qquad I = \frac{\mathcal{E}}{R} = 0 \qquad \mathbf{F} = I \int \mathrm{d}\mathbf{r}\times\mathbf{B} = \bO \]
