Oscilaciones forzadas

De Laplace

Revisión a fecha de 10:44 11 mar 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Solución estacionaria sinusoidal
- 2.1 Posición
  - 2.1.1 Amplitud
- 2.2 Velocidad
3 Dependencia con la frecuencia
- 3.1 Amplitud
- 3.2 Fase
4 Resonancia
- 4.1 Factor de calidad
5 Transitorio
6 Circuito RLC

1 Introducción

Un oscilador armónico amortiguado es aquel que, en adición a la fuerza recuperadora dada por la ley de Hooke, experimenta una fuerza de rozamiento viscoso proporcional a la velocidad.

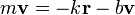
$m\mathbf{v}=-k\mathbf{r}-b\mathbf{v}\,$

Si este oscilador se mueve a lo largo de una recta, la segunda ley de Newton se reduce a

$ma = -kx - bv\,$

Si este oscilador amortiguado se encuentra sometido a una fuerza externa adicional, en general dependiente del tiempo, se dice que el oscilador está forzado, siendo su ecuación de movimiento

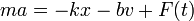
$ma = -kx - bv + F(t)\,$

De entre los posibles tipos de fuerza que se pueden aplicar, la más importante desde el punto de vista físico, es aquella que en sí misma es oscilante, esto es

$ma = -kx - bv + F_0\cos(\omega t)\,$

donde la frecuencia de oscilación de la fuerza no tiene por qué coincidir con la frecuencia propia del oscilador armónico

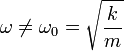
$\omega\neq \omega_0=\sqrt{\frac{k}{m}}$

2 Solución estacionaria sinusoidal

Si escribimos la ecuación de movimiento expresando la velocidad y la aceleración como derivadas de la posición nos queda la ecuación

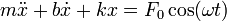
$m\ddot{x}+b\dot{x}+kx = F_0\cos(\omega t)$

El problema general consiste en determinar la elongación como función del tiempo, $x (t)$ para una posición y velocidad iniciales.

Antes de exponer la solución general, que se explica al final de este artículo, vamos a describir la solución particular más importante, que es la que se denomina estado estacionario sinusoidal, en la cual la elongación oscila con la misma frecuencia que la fuerza oscilante (no con su frecuencia propia, $ω 0$ ):

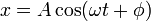
$x = A\cos(\omega t+\phi)\,$

El problema, para esta solución particular consiste en determinar la amplitud de las oscilaciones, $A$ , así como su desfase respecto a la fuerza aplicada $φ$ .

Esta solución es importante, porque se demuestra que, cualesquiera que sean las condiciones iniciales, el sistema termina por oscilar con esta solución particular.

2.1 Posición

La forma más sencilla de determinar la solución estacionaria sinusoidal es mediante el uso de fasores. La fuerza aplicada puede escribirse, con ayuda de la fórmula de Euler, como

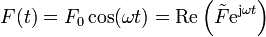
$F(t) = F_0\cos(\omega t)=\mathrm{Re}\left(\tilde{F}\mathrm{e}^{\mathrm{j}\omega t}\right)$

donde

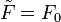
$\tilde{F}=F_0$

es el fasor, o amplitud compleja, de la fuerza. Es una cantidad compleja cuyo módulo nos da la amplitud de las oscilaciones ( $F 0$ en este caso) y cuyo argumento nos da el desfase (nulo, en este caso).

En la solución estacionaria sinusoidal, la elongación admite una expresión análoga

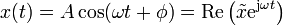
$x(t) = A\cos(\omega t+\phi)=\mathrm{Re}\left(\tilde{x}\mathrm{e}^{\mathrm{j}\omega t}\right)$

donde ahora

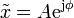
$\tilde{x}=A\mathrm{e}^{\mathrm{j}\phi}\,$

Este fasor contiene tanto la amplitud como la fase de la solución, por lo que si determinamos el fasor, ya hemos resuelto nuestro problema.

La ventaja de usar fasores es que transforma las derivadas en multiplicaciones. La velocidad y la aceleración pueden expresarse también en forma fasorial, siendo sus amplitudes complejas

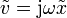
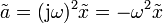
$\tilde{v}=\mathrm{j}\omega\tilde{x}$ $\tilde{a}=(\mathrm{j}\omega)^2\tilde{x}=-\omega^2\tilde{x}$

Puesto que en la ecuación de movimiento

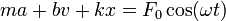
$ma + bv + kx = F_0\cos(\omega t)\,$

todas las cantidades ( $F$ , $x$ , $v$ y $a$ ) oscilan con la misma frecuencia, podemos escribirla como una relación entre fasores

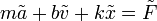
$m\tilde{a} + b\tilde{v} + k\tilde{x} = \tilde{F}$

Sustituyendo los fasores de la velocidad y la aceleración nos queda

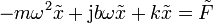
$-m\omega^2\tilde{x} +\mathrm{j} b\omega\tilde{x} + k\tilde{x} = \tilde{F}$

Esta es una ecuación algebraica de la cual es inmediato despejar el fasor de la elongación

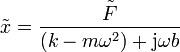
$\tilde{x}=\frac{\tilde{F}}{(k-m\omega^2)+\mathrm{j}\omega b}$

2.1.1 Amplitud

La amplitud de las oscilaciones la hallamos como el módulo del fasor. A su vez, el módulo de un cociente de números complejos es el cociente de los módulos, por lo que

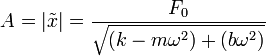
$A = \left|\tilde{x}\right| = \frac{F_0}{\sqrt{(k-m\omega^2)+(b\omega^2)}}$

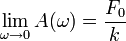
Esta amplitud es una función de la frecuencia. Para frecuencias bajas, la amplitud de las oscilaciones tiende a $\lim_{\omega\to 0} A(\omega) = \frac{F_0}{k}$

que es el comportamiento que uno obtiene para una fuerza no oscilante, como el peso, para el cual la frecuencia sería estrictamente nula.

Para frecuencias altas la amplitud tiende a cero

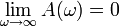
$\lim_{\omega\to \infty} A(\omega) = 0$

Esto quiere decir que si un oscilador lo excitamos mediante una fuerza cuya frecuencia sea mucho mayor que la propia del oscilador, éste prácticamente no se ve afectado.

Para valores intermedios de la frecuencia, de valor comparable a la frecuencia propia $ω 0$ , podemos tener un máximo de amplitud o no tenerlo dependiendo del grado de amortiguamiento.

Definiendo los parámetros

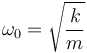
$\beta = \frac{b}{2m}$ $\omega_0=\sqrt{\frac{k}{m}}$

queda la amplitud

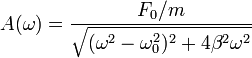
$A(\omega) = \frac{F_0/m}{\sqrt{(\omega^2-\omega_0^2)^2+4\beta^2\omega^2}}$

Esta función es máxima cuando lo que hay dentro de la raíz es mínimo, lo cual ocurre para

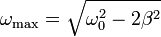
$\omega_\mathrm{max}=\sqrt{\omega_0^2-2\beta^2}$

como se comprueba sin más que derivar el radicando e igualar a cero.

Este resultado nos dice que para que haya un máximo en la amplitud debe ser

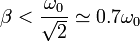
$\beta < \frac{\omega_0}{\sqrt{2}}\simeq 0.7 \omega_0$

esto es, no solo debe ser subamortiguado, sino con un amotiguamiento bastante inferior al crítico.

Si se cumple esta condición, la amplitud el máximo es

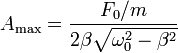
$A_\mathrm{max}=\frac{F_0/m}{2\beta\sqrt{\omega_0^2-\beta^2}}$

Esta amplitud máxima diverge cuando 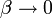$\beta\to 0$ . Se dice que el sistema posee una resonancia en la amplitud.

2.2 Velocidad

Obtenemos el fasor de la velocidad multiplicando el de la elongación por $jω$

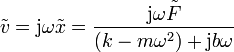
$\tilde{v}=\mathrm{j}\omega\tilde{x}=\frac{\mathrm{j}\omega \tilde{F}}{(k-m\omega^2)+\mathrm{j}b\omega}$

Dividiendo en el numerador y el denominador

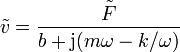
$\tilde{v}=\frac{\tilde{F}}{b+\mathrm{j}(m\omega-k/\omega)}$

la velocidad es también una función oscilante,

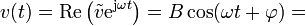
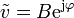
$v(t) = \mathrm{Re}\left(\tilde{v}\mathrm{e}^{\mathrm{j}\omega t}\right) = B\cos(\omega t + \varphi)=\,$ $\tilde{v}=B\mathrm{e}^{\mathrm{j}\varphi}$

cuya amplitud de oscilación es

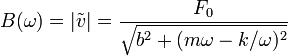
$B(\omega) = |\tilde{v}|=\frac{F_0}{\sqrt{b^2+(m\omega - k/\omega)^2}}$

De nuevo tenemos una función dependiente de la frecuencia.

Bajas frecuencias: Cuando 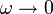$\omega\to 0$ , el término $k / ω$ tiende a infinito y la amplitud se va a cero. Esto quiere decir que para una fuerza que varía muy lentamente, el oscilador se mueve muy lentamente, de forma que en todo momento está casi en la posición de equilibrio calculada anteriormente.

Altas frecuencias: Cuando 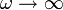$\omega\to \infty$ , es el término $m ω$ el que tiende a infinito y la amplitud se va de nuevo a cero. Esto quiere decir que para una fuerza que varía muy rápidamente, la inercia del oscilador le impide responder y este se limita a vibrar ligeramente alrededor de su posición de equilibrio $x = 0$ .

Resonancia: En la raíz que aparece en la amplitud hay una suma de dos términos positivos. El primero no se anula nunca, pero el segundo se hace cero si

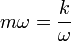
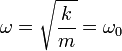
$m\omega = \frac{k}{\omega}$ $\Rightarrow$ $\omega = \sqrt{\frac{k}{m}} = \omega_0$

esto es, si la frecuencia de la fuerza aplicada coincide con la frecuencia propia del oscilador, la amplitud de las oscilaciones en la velocidad es máxima.

3 Dependencia con la frecuencia

3.1 Amplitud

3.2 Fase

4 Resonancia

4.1 Factor de calidad

5 Transitorio

6 Circuito RLC

Oscilaciones forzadas

De Laplace

Contenido

1 Introducción

2 Solución estacionaria sinusoidal

2.1 Posición

2.1.1 Amplitud

2.2 Velocidad

3 Dependencia con la frecuencia

3.1 Amplitud

3.2 Fase

4 Resonancia

4.1 Factor de calidad

5 Transitorio

6 Circuito RLC

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES