Momento cinético de un sistema de partículas

De Laplace

Revisión a fecha de 21:55 10 feb 2010; Gonfer (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Definición

De manera análoga a la cantidad de movimiento, se define el momento cinético (o angular) de un sistema de partículas como la suma vectorial de los momentos cinéticos individuales

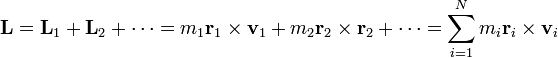
$\mathbf{L}=\mathbf{L}_1+\mathbf{L}_2 +\cdots = m_1\mathbf{r}_1\times\mathbf{v}_1+m_2\mathbf{r}_2\times\mathbf{r}_2+\cdots = \sum_{i=1}^N m_i\mathbf{r}_i\times\mathbf{v}_i$

1.1 Descomposición del momento angular

Las ecuaciones de la dinámica de sistemas se simplificarían notablemente si el momento angular, como el lineal, equivaliera al de una partícula puntual que concentrara toda la masa. No es así.

Para relacionar el momento angular con el centro de masa, descomponemos cada posición y cada velocidad en suma de la del centrode masa más la posición o velocidad relativas

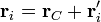
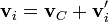
$\mathbf{r}_i = \mathbf{r}_C+\mathbf{r}'_i\,$ $\mathbf{v}_i = \mathbf{v}_C+\mathbf{v}'_i\,$

Con esta descomposición, el momento angular de cada partícula se separa en cuatro términos

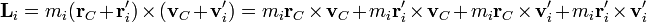
$\mathbf{L}_i = m_i(\mathbf{r}_C+\mathbf{r}'_i)\times( \mathbf{v}_C+\mathbf{v}'_i)= m_i\mathbf{r}_C\times\mathbf{v}_C+m_i\mathbf{r}'_i\times \mathbf{v}_C+m_i\mathbf{r}_C\times\mathbf{v}'_i+m_i\mathbf{r}'_i\times\mathbf{v}'_i$

Al sumar los momentos cinéticos individuales para obtener el momento angular total nos quedan cuatro sumas, en cada una de las cuales podemos sacar factor común la posición o la velocidad del CM, que es una cantidad que no depende del índice $i$

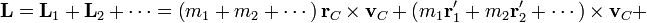
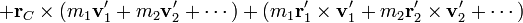
$\mathbf{L}= \mathbf{L}_1+\mathbf{L}_2 +\cdots = \left(m_1+m_2+\cdots\right)\mathbf{r}_C\times\mathbf{v}_C+\left(m_1\mathbf{r}'_1+m_2\mathbf{r}'_2+\cdots\right)\times\mathbf{v}_C +$ $+\mathbf{r}_C\times\left(m_1\mathbf {v}'_1+m_2\mathbf{v}'_2+\cdots\right)+\left(m_1\mathbf{r}'_1\times\mathbf{v}'_1+m_2\mathbf{r}'_2\times\mathbf{v}'_2+\cdots\right)$

Ahora bien, de la definición de centro de masas se deduce que

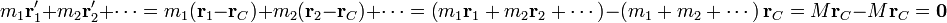
$m_1\mathbf{r}'_1+m_2\mathbf{r}'_2 +\cdots = m_1(\mathbf{r}_1-\mathbf{r}_C)+m_2(\mathbf{r}_2-\mathbf{r}_C)+\cdots = \left(m_1\mathbf{r}_1+m_2\mathbf{r}_2+\cdots\right)-\left(m_1+m_2+\cdots\right)\mathbf{r}_C = M\mathbf{r}_C-M\mathbf{r}_C = \mathbf{0}$

y, del mismo modo,

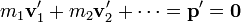
$m_1\mathbf{v}'_1 + m_2\mathbf{v}'_2 +\cdots = \mathbf{p}' = \mathbf{0}$

Por tanto, el segundo y el tercer término en la expresión del momento cinético total se anulan y la expresión se reduce a

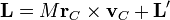
$\mathbf{L}= M\mathbf{r}_C\times\mathbf{v}_C+\mathbf{L}'$

donde

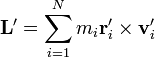
$\mathbf{L}'= \sum_{i=1}^N m_i\mathbf{r}'_i\times\mathbf{v}'_i$

es el momento angular relativo al centro de masas.

Según esto, el momento angular o cinético de un sistema de partículas se compone de dos contribuciones: el momento angular que tendría una partícula que contuviera toda la masa y se moviera como el centro de masas del sistema, más el momento angular que tienen las partículas por moverse alrededor del centro de masas.

Un ejemplo físico sencillo de esta descomposición lo tenemos en el momento angular de la Tierra en cuanto planeta del Sistema Solar. Su momento angular se compone de una parte debida al movimiento de traslación alrededor del Sol (lo que se conoce como momento angular orbital), que sería el primer término, más otra parte debida al movimiento de rotación alrededor de su eje (el llamado momento angular intrínseco), que sería 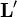$\mathbf{L}'$ .

2 Conservación del momento cinético

Derivando en la expresión del momento cinético de un sistema de partículas obtenemos

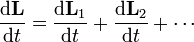
$\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t} = \frac{\mathrm{d}\mathbf{L}_1}{\mathrm{d}t} + \frac{\mathrm{d}\mathbf{L}_2}{\mathrm{d}t} + \cdots$

Para cada partícula la derivada del momento angular es el momento de las fuerzas aplicadas sobre ella:

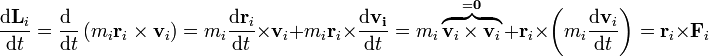
$\frac{\mathrm{d}\mathbf{L}_i}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(m_i\mathbf{r}_i\times\mathbf{v}_i\right) = m_i\frac{\mathrm{d}\mathbf{r}_i}{\mathrm{d}t}\times\mathbf{v}_i + m_i\mathbf{r}_i\times\frac{\mathrm{d}\mathbf{v_i}}{\mathrm{d}t} = m_i\overbrace{\mathbf{v}_i\times\mathbf{v}_i}^{=\mathbf{0}} + \mathbf{r}_i\times\left(m_i\frac{\mathrm{d}\mathbf{v}_i}{\mathrm{d}t}\right) = \mathbf{r}_i\times\mathbf{F}_i$

y, para el momento cinético total

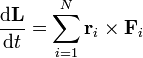
$\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}= \sum_{i=1}^N \mathbf{r}_i\times\mathbf{F}_i$

De nuevo, esta expresión requiere conocer las fuerzas internas del sistema, que son usualmente desconocidas. Por ello, descomponemos de nuevo en sumas de fuerzas externas e internas

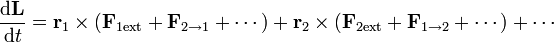
$\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}= \mathbf{r}_1\times\left(\mathbf{F}_{1\mathrm{ext}}+\mathbf{F}_{2\to 1}+\cdots\right) + \mathbf{r}_2\times\left(\mathbf{F}_{2\mathrm{ext}}+\mathbf{F}_{1\to 2}+\cdots\right)+ \cdots$

Pero si las fuerzas internas entre dos partículas no solo cumplen la tercera ley de Newton, sino que además son centrales, esto es, van en la dirección de la recta que une las dos partículas se verifica

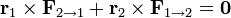
$\mathbf{r}_1\times\mathbf{F}_{2\to 1}+\mathbf{r}_2\times\mathbf{F}_{1\to 2}=\mathbf{0}$

Esta condición se cumple en la mayoría de los casos prácticos (fuerzas eléctricas o gravitatorias). En este caso, los momentos de las fuerzas internas se anulan dos a dos y queda

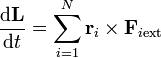
$\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}= \sum_{i=1}^N \mathbf{r}_i\times\mathbf{F}_{i\mathrm{ext}}$

En palabras:

La derivada del momento angular o cinético de un sistema de partículas es igual a la suma de los momentos de las fuerzas externas aplicadas sobre el sistema.

En particular, en un sistema de partículas sometido exclusivamente a fuerzas internas, el momento angular permanece constante.

Momento cinético de un sistema de partículas

De Laplace

1 Definición

1.1 Descomposición del momento angular

2 Conservación del momento cinético

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES