Entrar Página Discusión Historial Go to the site toolbox

Cantidad de movimiento de un sistema de partículas

De Laplace

Contenido

1 Definición

La cantidad de movimiento (o momento lineal) del sistema es la suma de las cantidades de movimiento de cada una de las partículas

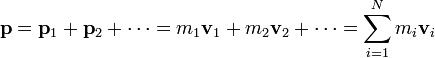
\mathbf{p} = \mathbf{p}_1+\mathbf{p}_2+\cdots = m_1\mathbf{v}_1+m_2\mathbf{v}_2 + \cdots = \sum_{i=1}^N m_i\mathbf{v}_i

2 Sistema centro de masas

La cantidad de movimiento se relaciona directamente con el centro de masas del sistema. Derivando respecto al tiempo la relación

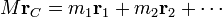
M\mathbf{r}_C = m_1 \mathbf{r}_1 + m_2\mathbf{r}_2+\cdots

obtenemos

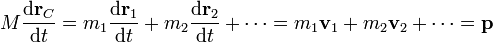
M \frac{\mathrm{d}\mathbf{r}_C}{\mathrm{d}t} = m_1 \frac{\mathrm{d}\mathbf{r}_1}{\mathrm{d}t} + m_2\frac{\mathrm{d}\mathbf{r}_2}{\mathrm{d}t} + \cdots = m_1\mathbf{v}_1+m_2\mathbf{v}_2+\cdots = \mathbf{p}

esto es

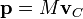
\mathbf{p} = M \mathbf{v}_C

En palabras: la cantidad de movimiento del sistema equivale a la que tendría una sola partícula material que concentrara toda la masa del sistema y que se moviera como el centro de masas de éste.

De la relación entre cantidad de movimiento y centro de masas se llega a que la cantidad de movimiento del sistema respecto al centro de masas es siempre nula

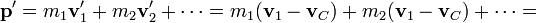
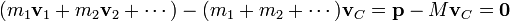
\mathbf{p}' = m_1 \mathbf{v}'_1 + m_2\mathbf{v}'_2 + \cdots = m_1 (\mathbf{v}_1-\mathbf{v}_C) + m_2(\mathbf{v}_1-\mathbf{v}_C) + \cdots = ( m_1\mathbf{v}_1+m_2\mathbf{v}_2 + \cdots) - (m_1+m_2+\cdots)\mathbf{v}_C = \mathbf{p}- M \mathbf{v}_C=\mathbf{0}

Esto permite redefinir el centro de masas como aquel punto (variable) desde el cual la cantidad de movimiento del sistema es nula en todo momento. Cuando un sistema de partículas se estudia empleando este punto como origen del sistema de referencia se dice que se está estudiando desde el sistema centro de masas.

3 Conservación de la cantidad de movimiento

Supongamos un sistema de partículas sometidas a fuerzas externas y también interactuantes entre sí, cumpliendo las fuerzas internas la tercera ley de Newton. En este caso, la variación en el tiempo de la cantidad de movimiento total es

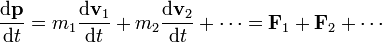
\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t} = m_1\frac{\mathrm{d}\mathbf{v}_1}{\mathrm{d}t}+ m_2\frac{\mathrm{d}\mathbf{v}_2}{\mathrm{d}t}+\cdots = \mathbf{F}_1+\mathbf{F}_2 + \cdots

esto es, la derivada de la cantidad de movimiento es la resultante de todas las fuerzas que actúan sobre las partículas del sistema. Esto es consecuencia directa de la definición, pero es poco útil pues requiere conocer también las fuerzas internas que son normalmente desconocidas. Por ello, descomponemos las fuerzas sobre cada partícula en suma de las externas y de las internas

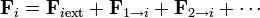
\mathbf{F}_i = \mathbf{F}_{i\mathrm{ext}}+\mathbf{F}_{1\to i}+\mathbf{F}_{2\to i}+\cdots

y la derivada de la cantidad de movimiento queda

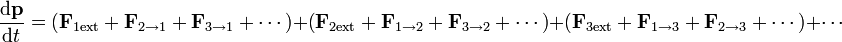
\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}=\left(\mathbf{F}_{1\mathrm{ext}}+\mathbf{F}_{2\to 1}+\mathbf{F}_{3\to 1}+\cdots\right)+\left(\mathbf{F}_{2\mathrm{ext}}+\mathbf{F}_{1\to 2}+\mathbf{F}_{3\to 2}+\cdots\right)+\left(\mathbf{F}_{3\mathrm{ext}}+\mathbf{F}_{1\to 3}+\mathbf{F}_{2\to 3}+\cdots\right)+\cdots

Pero, de acuerdo con la tercera ley de Newton

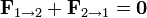
\mathbf{F}_{1\to 2}+\mathbf{F}_{2\to 1} = \mathbf{0}

y análogamente para el resto de pares de partículas. Por tanto, las fuerzas internas se cancelan dos a dos y queda la expresión mucho más útil

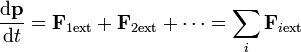
\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}= \mathbf{F}_{1\mathrm{ext}}+\mathbf{F}_{2\mathrm{ext}}+\cdots = \sum_i \mathbf{F}_{i\mathrm{ext}}

esto es:

  • la derivada de la cantidad de movimiento es igual a la resultante de las fuerzas externas aplicadas sobre el sistema.
  • En particular: En ausencia de fuerzas externas, la cantidad de movimiento de un sistema de partículas permanece constante.

En términos del centro de masas, la ley de evolución de la cantidad de movimiento se escribe

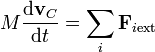
M\frac{\mathrm{d}\mathbf{v}_C}{\mathrm{d}t} = \sum_i \mathbf{F}_{i\mathrm{ext}}

es decir:

  • El centro de masas de un sistema de partículas se mueve como una sola partícula cuya masa fuera la total del sistema y que se ecnontrara sometida a la resultante de las fuerzas externas ejercidas sobre el sistema.
  • En particular, el centro de masas de un sistema de partículas sometidas exclusivamente a fuerzas internas permanece en reposo o en un estado de movimiento uniforme.

Consideremos el ejemplo siguiente: un proyectil se lanza desde un mortero. El proyectil describe (despreciando la resistencia del aire) una trayectoria parabólica. En cierto punto del vuelo el proyectil explota en multitud de fragmentos. El centro de masas de estos fragmentos continúa el movimiento parabólico inicial.

Este principio imposibilita que, por ejemplo, un grupo de aguerridos astronautas consiga desviar la trayectoria de un cometa simplemente colocando una bomba en él, ya que las fuerzas debidas a la bomba son puramente internas, y el centro de masas continuará su trayectoria inalterada, por mucho que se fragmente el asteroide.

4 Ejemplos

4.1 Colisiones

4.2 Explosión de un proyectil

4.3 Propulsión a reacción

5 Aplicación a colisiones

Obtenido de "http://tesla.us.es/wiki/index.php/Cantidad_de_movimiento_de_un_sistema_de_part%C3%ADculas"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace