Movimiento armónico simple

De Laplace

Revisión a fecha de 19:16 9 feb 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 Combinación de funciones trigonométricas
3 Amplitud y fase
- 3.1 Relación con la combinación lineal
4 Posición, velocidad y aceleración en un MAS
5 Amplitud compleja (fasor)

1 Introducción

El movimiento armónico simple (o, abreviadamente, M.A.S.) es el descrito por una partícula que se mueve a lo largo de una recta verificando la ley de Hooke

$\mathbf{F} = - k\mathbf{r}\,$

Por tratarse de un movimiento rectilíneo, puede reducirse el movimiento a una sola componente

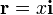
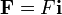
$\mathbf{r}=x\mathbf{i}$ $\mathbf{F}=F\mathbf{i}\,$

de forma que la ecuación de movimiento se reduce a

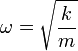
$\ddot{x}= -\frac{k}{m}x=-\omega^2x$ $\omega=\sqrt{\frac{k}{m}}$

La solución de esta ecuación diferencial, con las condiciones iniciales

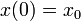
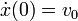
$x(0)=x_0\,$ $\dot{x}(0)=v_0$

es la forma general de un movimiento armónico simple.

2 Combinación de funciones trigonométricas

Para resolver la ecuación de movimiento de un oscilador armónico, empleando técnicas elementales, observamos que trata de hallar una función cuya segunda derivada sea proporcional a la propia función. Es fácil encontrar dos funciones que cumplen esta condición

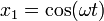
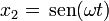
$x_1 = \cos(\omega t)\,$ $x_2 = \,\mathrm{sen}(\omega t)$

Por simple sustitución comprobamos que se cumple

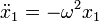
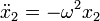
$\ddot{x}_1 = -\omega^2x_1$ $\ddot{x}_2 = -\omega^2x_2$

Ninguna de estas dos soluciones particulares puede ser la solución general, ya que no cumplen las condiciones iniciales del movimiento. Sin embargo, una combinación lineal de ellas sí lo es. Multiplicando cada una por una constante y sumando, tenemos que

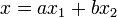
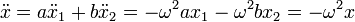
$x = ax_1 + bx_2\,$ $\Rightarrow$ $\ddot{x}=a\ddot{x}_1+b\ddot{x}_2 = -\omega^2ax_1-\omega^2 b x_2 = -\omega^2x$

El valor de estas dos constantes, $a$ y $b$ lo dan las condiciones iniciales. Al resultar un sistema de dos ecuaciones con dos incógnitas, la solución queda completamente determinada. Por tanto, la forma general del movimiento armónico simple es

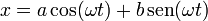
$x = a\cos(\omega t) + b\,\mathrm{sen}(\omega t)$

Derivando esta ecuación obtenemos la velocidad instantánea

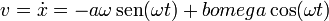
$v =\dot{x}= -a\omega\,\mathrm{sen}(\omega t)+bºomega\cos(\omega t)$

Imponiendo las condiciones iniciales obtenemos $a$ y $b$ . De la posición inicial

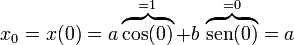
$x_0 = x(0) = a\overbrace{\cos(0)}^{=1} + b\,\overbrace{\mathrm{sen}(0)}^{=0} = a$ $\Rightarrow$ $a = x_0\,$

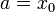
y de la velocidad inicial

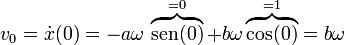
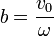
$v_0 = \dot{x}(0) = -a\omega\,\overbrace{\mathrm{sen}(0)}^{=0} + b\omega\overbrace{\cos(0)}^{=1} = b\omega$ $\Rightarrow$ $b = \frac{v_0}{\omega}$

con lo que la solución general, en función de la posición y la velocidad inicial es

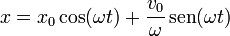
$x = x_0\cos(\omega t) + \frac{v_0}{\omega}\,\mathrm{sen}(\omega t)$

3 Amplitud y fase

Una forma alternativa de escribir la solución general del movimiento armónico simple es

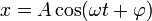
$x = A\cos(\omega t+\varphi)$

donde $A$ y $\varphi$ son dos constantes que se pueden obtener a partir de las condiciones iniciales. Estas dos constantes, dada su importancia, poseen nombre propio:

$A$ es la amplitud.

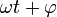$\varphi$ es la constante de fase (siendo $\omega t + \varphi$ la fase del movimiento)

3.1 Relación con la combinación lineal

Es sencillo demostrar la equivalencia entre las dos expresiones de la solución general. Aplicando la expresión del coseno de una suma

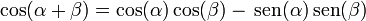
$\cos(\alpha+\beta) = \cos(\alpha)\cos(\beta)-\,\mathrm{sen}(\alpha)\,\mathrm{sen}(\beta)$

obtenemos

$x = A\cos(\omega t)\cos(\varphi)-A\,\mathrm{sen}(\omega t)\,\mathrm{sen}(\varphi)$

que es idéntica a la expresión dada en la sección anterior

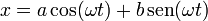
$x = a\cos(\omega t)+b\,\mathrm{sen}(\omega t)$

si se verifica la relación entre las constantes

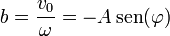
$a = x_0 = A\cos(\varphi)\,$ $b = \frac{v_0}{\omega}=-A\,\mathrm{sen}(\varphi)$

La relación inversa a ésta nos permite hallar la amplitud y la constante de fase en función de las condiciones iniciales

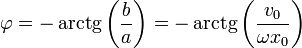
$A = \sqrt{a^2+b^2}=\sqrt{x_0^2 + \frac{v_0^2}{\omega^2}}$ $\varphi=-\,\mathrm{arctg}\left(\frac{b}{a}\right)=-\,\mathrm{arctg}\left(\frac{v_0}{\omega x_0}\right)$

Gráficamente, podemos representar un vector $\mathbf{A}$ en dos dimensiones, cuyas componentes cartesianas son las constantes $a$ y $b$

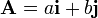
$\mathbf{A}=a\mathbf{i}+b\mathbf{j}\,$

Este vector tiene por módulo la amplitud de las oscilaciones, y el ángulo que forma con el eje X es la constante de fase $\varphi$

4 Posición, velocidad y aceleración en un MAS

5 Amplitud compleja (fasor)

Artículo completo: Fasor

Existe otra forma alternativa de expresar el movimiento armónico simple. La fórmula de Euler establece una relación entre la exponencial de un número imaginario y las funciones trigonométricas

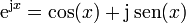
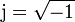
$\mathrm{e}^{\mathrm{j}x} = \cos(x)+\mathrm{j}\,\mathrm{sen}(x)$ $\mathrm{j}=\sqrt{-1}$

o, equivalentemente,

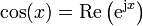
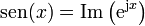
$\cos(x) = \mathrm{Re}\left(\mathrm{e}^{\mathrm{j}x}\right)$ $\mathrm{sen}(x) = \mathrm{Im}\left(\mathrm{e}^{\mathrm{j}x}\right)$

Aplicando esta relación a la solución general del M.A.S. obtenemos

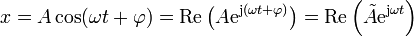
$x = A \cos(\omega t + \varphi) = \mathrm{Re}\left(A \mathrm{e}^{\mathrm{j}(\omega t + \varphi)}\right) = \mathrm{Re}\left(\tilde{A}\mathrm{e}^{\mathrm{j}\omega t}\right)$

donde

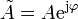
$\tilde{A}=A\mathrm{e}^{\mathrm{j}\varphi}$

es la llamada amplitud compleja o fasor de la variable $x$ . Es un número complejo cuyo módulo es la amplitud del movimiento y cuyo argumento es la constante de fase.

Aplicando de nuevo la fórmula de Euler obtenemos la parte real y la imaginaria del fasor

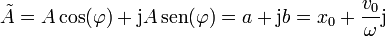
$\tilde{A}= A\cos(\varphi)+\mathrm{j}A\,\mathrm{sen}(\varphi)=a+\mathrm{j}b=x_0+\frac{v_0}{\omega}\mathrm{j}$

esto es, la amplitud compleja queda completamente determinada por las condiciones iniciales. Vemos que el vector de componentes $a$ y $b$ que definimos anteriormente no es más que la representación del fasor en el plano complejo.

Movimiento armónico simple

De Laplace

Contenido

1 Introducción

2 Combinación de funciones trigonométricas

3 Amplitud y fase

3.1 Relación con la combinación lineal

4 Posición, velocidad y aceleración en un MAS

5 Amplitud compleja (fasor)

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES