Principios de la dinámica

De Laplace

Revisión a fecha de 13:32 7 feb 2010; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Introducción

Los principios de la dinámica o Leyes de Newton son los axiomas por los que se rigen las partículas y sistemas en la dinámica clásica. Fueron enunciados por Newton, basándose en los trabajos de Galileo, en sus Principia Mathematica.

Una versión de estos principios, enunciada de forma moderna, es la siguiente:

2 Principio de inercia

El primer principio de la dinámica, también conocido como Primera Ley de Newton puede formularse como

“Toda partícula libre de interacciones permanece en reposo o en estado de movimiento rectilíneo y uniforme.”

Normalmente se formula usando “fuerzas” en lugar de “interacciones” pero puesto que ello requiere el haber definido previamente el concepto de fuerza, es preferible enunciarlo de una manera más genérica.

Este principio fue enunciado inicialmente por Galileo.

Lo que nos dice esta ley es que el espacio es euclídeo ya que las trayectorias de las partículas libres son rectas y no circunferencias (como ocurriría en la superficie de una esfera). El primer principio permite definir sistemas de referencia ortogonales que se extienden indefinidamente en el espacio y en el tiempo.

El primer principio de la dinámica nos permite definir los sistemas de referencia inerciales como aquellos en que una partícula libre sigue un movimiento rectilíneo y uniforme.

El principio de inercia se ve modificado en la teoría general de la relatividad, que corrige y generaliza las leyes de Newton. En su versión más general, una partícula libre no sigue necesariamente un movimiento rectilíneo y uniforme, sino que se desplza siguiendo una geodésica. En el marco de la relatividad general, el principio de inercia no es un postulado separado, sino que es una consecuencia del segundo principio.

3 Segunda Ley de Newton

El segundo principio de la dinámica requiere previamente la definición de la cantidad de movimiento 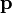$\mathbf{p}$ de una partícula, como

$\mathbf{p}=m\mathbf{v}$

de manera que la ley se enuncia

“La derivada de la cantidad de movimiento de una partícula es igual a la resultante de las fuerzas aplicadas sobre ella.”

En forma matemática

$\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t}=\dot{\mathbf{p}} = \sum_i \mathbf{F}_i$

En la mayoría de las ocasiones, la masa de una partícula es una constante por lo que la derivada de la cantidad de movimiento es igual a

$\frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t} = \overbrace{\frac{\mathrm{d}m}{\mathrm{d}t}}^{=0}\mathbf{v}+m\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t} = m \mathbf{a}$

de donde llegamos a la forma habitual de expresar la segunda ley de Newton

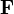$\mathbf{F}=m\mathbf{a}\,$

con $\mathbf{F}$ la resultante de las fuerzas aplicadas sobre la partícula.

Esta ley requiere el conocimiento de las fuerzas aplicadas, como un dato del problema. Estas fuerzas deben ser obtenidas independientemente para que la ley tenga verdadero significado. Por ello, precisamos de algún modelo físico que nos proporcione la expresión de la fuerza. Entre estos modelos se encuentran:

La ley de Hooke, para el oscilador armónico

$\mathbf{F}=-k\mathbf{r}\,$

La ley de la gravitación universal, para el movimiento de una masa en el campo gravitatorio de otra

$\mathbf{F}=-G\frac{m_1m_2(\mathbf{r}_2-\mathbf{r}_1)}{|\mathbf{r}_2-\mathbf{r}_1|^3}$

Esta ley contiene al caso particular e importante del movimiento de una masa pequeña en las proximidades de la superficie terrestre

$\mathbf{F}=m\mathbf{g}\,$

La ley de Lorentz, para el movimiento de una partícula en un campo electromagnético

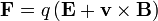
$\mathbf{F}=q\left(\mathbf{E}+\mathbf{v}\times\mathbf{B}\right)\,$

Un caso particular de esta ley es la ley de Coulomb, para la fuerza producida por una carga en reposo

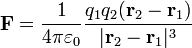
$\mathbf{F}=\frac{1}{4\pi\varepsilon_0}\frac{q_1q_2(\mathbf{r}_2-\mathbf{r}_1)}{|\mathbf{r}_2-\mathbf{r}_1|^3}$

Una característica común a todas estas leyes de fuerza es que proporcionan una fuerza dependiente de la posición y de la velocidad instantáneas de la partícula. Por ello, matemáticamente, la segunda ley de Newton proporciona la ecuación de movimiento como una ecuación diferencial