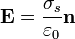Consecuencias del equilibrio electrostático

De Laplace

1 Introducción

Como consecuencia de la condición de equilibrio electrostático

• El campo eléctrico es nulo en el material conductor
• El material conductor es equipotencial.
• No hay densidad de carga de volumen en el material.
• Toda la carga está almacenada en las superficies del conductor.
• No hay líneas de campo que vayan de un conductor a él mismo.
• El campo justo fuera del conductor es perpendicular a la superficie.
• El campo justo fuera del condductor es de la forma

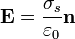
Veamos cada una de estas propiedades por separado.

2 Anulación del campo

La condición de equilibrio electrostático requiere que las cargas se encuentren reposo en el material conductor. Esto es, no se mueven, pese a que podrían hacerlo (pues un material conductor permite el desplazamiento de carga por su interior).

Si las cargas se encuentran en equilibrio, la fuerza sobre cada una de ellas debe ser nula

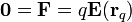
Puesto que esto tiene que ser cierto para cada carga en cualquier punto del interior del material conductor, ello implica que

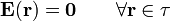
siendo τ el volumen de material conductor.

Esta es la propiedad básica que caracteriza a los conductores en equilibrio electrostático. Todas las demás que veremos se deducen de ella.

Hay que insistir que esta propiedad se cumple para un conductor en equilibrio. Si el conductor no está en equilibrio, porque está circulando una corriente por su interior, entonces no es cierto que 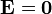. No hay que pensar que, por el simple hecho de ser conductor, ya el campo se anula en un material. La misma salvedad al resto de las propiedades que siguen.

3 Equipotencialidad

4 Densidad volumétrica nula

5 Densidad superficial no nula

6 Líneas de campo prohibidas

7 Ortogonalidad a la superficie

8 Proporcionalidad a σ_s