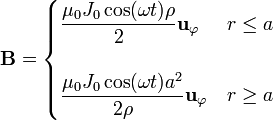Campo eléctrico inducido por un cable grueso
De Laplace
Revisión a fecha de 11:42 1 dic 2009; Antonio (Discusión | contribuciones)
Contenido |
1 Enunciado
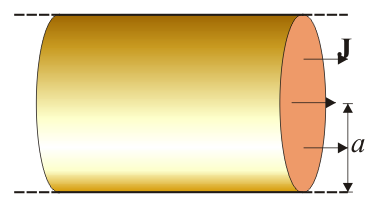
Por un hilo rectilíneo cilíndrico de radio a y gran longitud circula una corriente alterna de baja frecuencia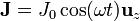 .
.
- Halle el campo magnético producido por este hilo, tanto en su interior como en su exterior, suponiendo que la corriente es casi estacionaria.
- Halle el campo eléctrico inducido por este campo magnético tanto en el interior del cable como en su exterior, suponiendo que
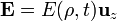 y que en el eje del cilindro el campo eléctrico es nulo.
y que en el eje del cilindro el campo eléctrico es nulo.
- Calcule la densidad de corriente de desplazamiento en el interior y el exterior del hilo.
2 Campo magnético debido al cable
Al tratarse de una corriente casi estacionaria, el campo magnético puede calcularse como en el caso de un cable grueso recorrido por una corriente continua. Tal como se ve en el tema de campo magnético de corrientes estacionarias, el campo que produce este cable es