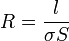Resistencia de un tubo
De Laplace
Contenido |
1 Enunciado
Sea un tubo cilíndrico, de radio interior a y exterior b, y longitud h, de un material de conductividad σ. Calcule la resistencia eléctrica- Entre las dos bases.
- Entre la cara interior y la exterior.
2 Introducción
A la hora de hablar de la resistencia de un conductor, tan importante como dar las dimensiones de la pieza es definir de dónde a dónde fluye la corriente. Hay veces en que esto es evidente (por ejemplo, en un conductor filiforme, parece natural que la corriente fluya de un extremo al otro), pero no siempre es así.
Consideremos un cilindro hueco como en este problema.
- Este cilindro puede ser parte de un cable bimetálico, por ejemplo, un cable de cobre con un núcleo de acero para darle rigidez, como los que se emplean en algunos tendidos de gran longitud. En este cable bimetálico, la corriente fluye a lo largo del cobre principalmente (pues el acero es mucho más resistivo) y debemos considerar la resistencia entre las bases.
- Alternativamente, este cilindro puede representar el dieléctrico que se encuentra entre los conductores de un cable coaxial. Este dieléctrico se supone perfectamente aislante, pero en realidad suele tener una pequeña conductividad. En este caso, existen corrientes de fuga que van desde el conductor interior al exterior, radialmente. La resistencia del cilindro debe calcularse entre su superficie interior y la exterior.
3 Resistencia longitudinal
La resistencia de un tubo se calcula suponiendo una diferencia de potencial entre sus extremos y hallando la corriente que fluye. Por ser el material homogéneo, la ecuación que verifica el potencial es la de Laplace

Empleando coordenadas cilíndricas con z la dirección longitudinal queda
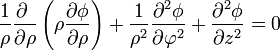
A esta ecuación debemos añadir las condiciones de contorno de que en los extremos haya una diferencia de potencial V0,

Además de estas condiciones hay que fijar las condiciones en las paredes laterales. En estas se verifica que la corriente que sale es nula (no hay fugas) y, por tanto,
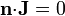

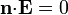

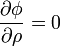
esto es, en las caras laterales se cumple que la derivada del potencial en la dirección perpendicular (radial en este caso) es nula.
Una solución para este problema es un potencial que varía linealmente con z
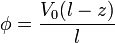
Este potencial obedece la ecuación de Laplace y satisface las condiciones de contorno tanto en las bases como en las caras laterales. por tanto, es la solución.
Conocido el potencial, hallamos el campo y la corriente
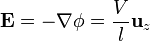
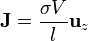
Resulta un campo y una corriente uniformes en la dirección longitudinal.
Integrando ahora sobre una sección transversal resulta
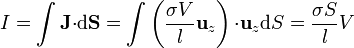
de donde la resistencia es