Entrar Página Discusión Historial Go to the site toolbox

Campo magnético de una esfera rotatoria

De Laplace

Contenido

1 Enunciado

Una esfera de radio a almacena una carga Q distribuida uniformemente en su superficie. La esfera gira con velocidad angular ω alrededor de un eje.

  1. Determine la densidad de corriente en la esfera
  2. Calcule, por integración directa, el campo magnético en los puntos del eje de rotación.
  3. Calcule el momento dipolar magnético de la esfera. A partir de aquí, halle el campo en puntos alejados de la esfera, no necesariamente en el eje.
  4. Halle, resolviendo las ecuaciones de la magnetostática, el campo en todos los puntos del espacio.

2 Densidad de corriente

Puesto que la densidad de carga se encuentra sobre la superficie de la esfera, la densidad de corriente resultante va a ser una superficial, 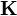\mathbf{K}. Si tenemos una distribución de carga superficial fijada en un sólido, el cual se mueve con velocidad \mathbf{v}, la densidad de corriente será

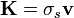
\mathbf{K}=\sigma_s\mathbf{v}\,

puesto que todos los portadores de carga de un elemento de superficie se mueven con la misma velocidad.

Para el caso de distribución uniforme

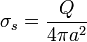
\sigma_s=\frac{Q}{4\pi a^2}

y un movimiento de rotación, empleando coordenadas esféricas

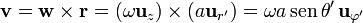
\mathbf{v}=\mathbf{w}\times\mathbf{r}=(\omega \mathbf{u}_z)\times(a\mathbf{u}_{r'})=\omega a\,\mathrm{sen}\,\theta'\,\mathbf{u}_{\varphi'}

y esto nos da la densidad de corriente

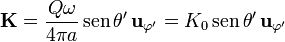
\mathbf{K}=\frac{Q\omega}{4\pi a}\,\mathrm{sen}\,\theta'\,\mathbf{u}_{\varphi'}=K_0\,\mathrm{sen}\,\theta'\,\mathbf{u}_{\varphi'}

3 Campo en el eje

4 Momento dipolar

4.1 A partir de la corriente

El momento dipolar magnético para una distribución de corriente superficial es

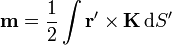
\mathbf{m}=\frac{1}{2}\int \mathbf{r}'\times\mathbf{K}\,\mathrm{d}S'

Empleando coordenadas esféricas, cada uno de los términos de esta integral valen

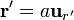
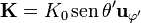
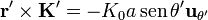
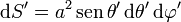
\mathbf{r}'=a\mathbf{u}_{r'}        \mathbf{K}=K_0\,\mathrm{sen}\,\theta'\mathbf{u}_{\varphi'}        \mathbf{r}'\times\mathbf{K}'=-K_0a\,\mathrm{sen}\,\theta'\mathbf{u}_{\theta'}        \mathrm{d}S'=a^2\,\mathrm{sen}\,\theta'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'

Puesto que se trata de una integral vectorial, hay que pasar a la base cartesiana, ya que, en esféricas,

Los vectores de la base dependen de la posición

Aplicamos que

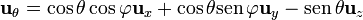
\mathbf{u}_{\theta}=\cos\theta\cos\varphi\mathbf{u}_{x}+\cos\theta\mathrm{sen}\,\varphi\mathbf{u}_{y}-\mathrm{sen}\,\theta\mathbf{u}_{z}

y la integral se puede descomponer en esta base

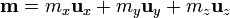
\mathbf{m}=m_x\mathbf{u}_x+m_y\mathbf{u}_y+m_z\mathbf{u}_z

con

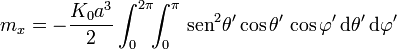
m_x=-\frac{K_0a^3}{2}\int_0^{2\pi}\!\!\int_0^\pi\,\mathrm{sen}^2\theta'\cos\theta'\,\cos\varphi'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'
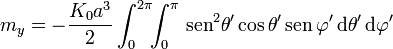
m_y=-\frac{K_0a^3}{2}\int_0^{2\pi}\!\!\int_0^\pi\,\mathrm{sen}^2\theta'\cos\theta'\,\mathrm{sen}\,\varphi'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'
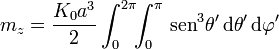
m_z=\frac{K_0a^3}{2}\int_0^{2\pi}\!\!\int_0^\pi\,\mathrm{sen}^3\theta'\,\mathrm{d}\theta'\,\mathrm{d}\varphi'

las dos primeras integrales se anulan ya que

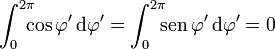
\int_0^{2\pi}\!\!\!\!\cos\varphi'\,\mathrm{d}\varphi'=\int_0^{2\pi}\!\!\!\mathrm{sen}\,\varphi'\,\mathrm{d}\varphi'=0

La tercera componente se convierte en un producto de dos integrales independientes

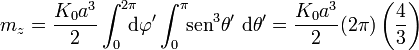
m_z=\frac{K_0a^3}{2}\int_0^{2\pi}\!\!\!\!\mathrm{d}\varphi'\int_0^\pi\!\!\mathrm{sen}^3\theta'\,\,\mathrm{d}\theta'=\frac{K_0a^3}{2}(2\pi)\left(\frac{4}{3}\right)

Simplificando nos queda el momento dipolar magnético

\mathbf{m}=\frac{4\pi K_0a^3}{3}\mathbf{u}_z=\frac{Q\omega a^2}{3}\mathbf{u}_z

4.2 A partir del campo magnético

4.3 Campo lejos de la esfera

5 Campo en todo el espacio

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_magn%C3%A9tico_de_una_esfera_rotatoria"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace