Partícula magnética en un campo externo

De Laplace

Revisión a fecha de 14:30 30 mar 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Magnetización y campo
3 Diamagnéticos y paramagnéticos
4 Corrientes de imanación
5 Casos particulares

1 Enunciado

Supóngase que se tiene una esfera de radio $R$ un material magnético lineal (de permeabilidad $μ$ ) alrededor de la cual hay vacío. En puntos alejados de la esfera hay impuesto un campo magnético uniforme $\mathbf{B}_0$ .

Sabiendo que la magnetización que aparece en la esfera es uniforme, halle el valor de dicha magnetización, del momento dipolar inducido en la esfera, y del campo magnético en todos los puntos del espacio.
¿En qué se diferencia el resultado para un material diamagnético de uno paramagnético? ¿A qué se reducen los resultados en los casos de un paramagnético ideal ( 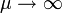$\mu\to\infty$ ) y un superconductor ( $μ = 0$ )?
Halle las corrientes de magnetización que aparecen en la esfera.
Calcule los valores numéricos para los apartados anteriores con un campo externo $B 0 = 10mT$ aplicado sobre una esfera de radio 1 cm para los siguientes materiales: oro, aluminio, hierro y un superconductor.

2 Magnetización y campo

Este problema tiene una total analogía con el correspondiente problema para dieléctricos.

La idea es que el campo externo, induce una magnetización en la esfera. Esta magnetización genera un campo, que es uniforme en el interior, y que también debe incluirse en los cálculos.

En el interior de la esfera el campo será la suma del externo y del debido a la magnetización. Este último, para una magnetización uniforme, vale

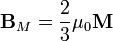
$\mathbf{B}_M=\frac{2}{3}\mu_0\mathbf{M}$

con lo que el campo total es

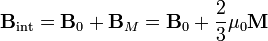
$\mathbf{B}_\mathrm{int}=\mathbf{B}_0+\mathbf{B}_M=\mathbf{B}_0+\frac{2}{3}\mu_0\mathbf{M}$

La magnetización, por su parte, es proporcional al campo total en el interior de la esfera. Aplicando que

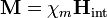
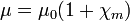
$\mathbf{M}=\chi_m\mathbf{H}_\mathrm{int}\,$ $\mu=\mu_0(1+\chi_m)\,$ $\mathbf{B}_\mathrm{int}=\mu\mathbf{H}_\mathrm{int}\,$

resulta

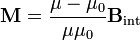
$\mathbf{M}=\frac{\mu-\mu_0}{\mu\mu_0}\mathbf{B}_\mathrm{int}$

sustituyendo en la expresión anterior, queda la ecuación para $\mathbf{B}$ .

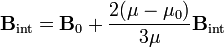
$\mathbf{B}_\mathrm{int}=\mathbf{B}_0+\frac{2(\mu-\mu_0)}{3\mu}\mathbf{B}_\mathrm{int}$

y despejando, obtenemos el campo en el interior de la esfera

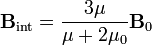
$\mathbf{B}_\mathrm{int}=\frac{3\mu}{\mu+2\mu_0}\mathbf{B}_0$

Conocido el campo tenemos la magnetización de la esfera

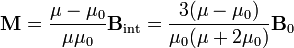
$\mathbf{M}=\frac{\mu-\mu_0}{\mu\mu_0}\mathbf{B}_\mathrm{int}=\frac{3(\mu-\mu_0)}{\mu_0(\mu+2\mu_0)}\mathbf{B}_0$

y el momento magnético de la esfera, por ser la magnetización uniforme

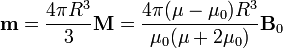
$\mathbf{m}=\frac{4\pi R^3}{3}\mathbf{M} = \frac{4\pi(\mu-\mu_0)R^3}{\mu_0(\mu+2\mu_0)}\mathbf{B}_0$

El campo magnético en el exterior de la esfera es la superposición del campo externo y del debido a un dipolo puntual en el centro de la esfera.

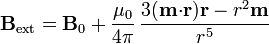
$\mathbf{B}_\mathrm{ext}=\mathbf{B}_0+\frac{\mu_0}{4\pi}\,\frac{3(\mathbf{m}{\cdot}\mathbf{r})\mathbf{r}-r^2\mathbf{m}}{r^5}$

3 Diamagnéticos y paramagnéticos

La diferencia entre un material y uno diamagnético y uno paramagnético es en el signo de la magnetización. Los diamagnéticos poseen una susceptibilidad negativa ( $χ m < 0$ , $μ < μ 0$ ) lo que hace que la magnetización vaya en sentido opuesto al campo aplicado. Los paramagnéticos, en cambio, poseen una susceptibilidad positiva, y la magnetización va en el mismo sentido que el campo aplicado.

Por ello, en un material diamagnético el campo interior es menor que el externo, mientras que en uno paramagnético se ve reforzado.

Los casos límite son los de una sustancia paramagnética ideal, que posee una susceptibilidad infinita. En este caso 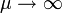$\mu\to\infty$ y el campo en el interior se convierte en

$\mathbf{B}_\mathrm{int} \to 3\mathbf{B}_0$

mientras que la magnetización y el momento dipolar valen

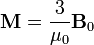
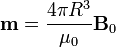
$\mathbf{M}=\frac{3}{\mu_0}\mathbf{B}_0$ $\mathbf{m}=\frac{4\pi R^3}{\mu_0}\mathbf{B}_0$

Es significativo que para un material paramagnético perfecto, el campo magnético $\mathbf{H}$ se anula en el interior de la esfera y el campo $\mathbf{B}$ (y $\mathbf{H}$ ) exterior es normal a la superficie de la esfera.

El otro caso extremo es el de un superconductor, que se comporta como un diamagnético perfecto, con permeabilidad nula ( $μ = 0$ ), anulándose el campo en el interior de la esfera

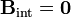
$\mathbf{B}_\mathrm{int}=\mathbf{0}$

y la magnetización y el momento dipolar valen

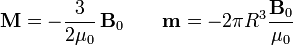
$\mathbf{M}=-\frac{3}{2\mu_0}\,\mathbf{B}_0\qquad \mathbf{m}=-2\pi R^3\frac{\mathbf{B}_0}{\mu_0}$

Hay que señalar que, para un superconductor, no es ésta la única descripción posible. Aquí hemos caracterizado el superconductor como un material en el que aparece una magnetización que anula el campo en el interior de la esfera.

Una descripción alternativa, y más realista, es la que considera que la anulación se produce por corrientes libres (no de magnetización) que aparecen en la superficie del superconductor.

4 Corrientes de imanación

Las corrientes de magnetización las hallamos a partir de la magnetización calculada. Dado que la magnetización de la esfera es uniforme, este cálculo es idéntico al del iman esférico. Resulta una corriente de volumen nula

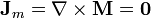
$\mathbf{J}_m = \nabla\times \mathbf{M} = \mathbf{0}$

y una de superficie en dirección acimutal

$\mathbf{K}_m = \mathbf{n}\times[\mathbf{M}] = \mathbf{u}_{r}\times(\mathbf{0} -M_0\mathbf{u}_{z}) = M_0\,\mathrm{sen}\,\theta\,\mathbf{u}_{\varphi}$

En función del campo externo, esta corriente vale

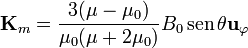
$\mathbf{K}_m = \frac{3(\mu-\mu_0)}{\mu_0(\mu+2\mu_0)}B_0\,\mathrm{sen}\,\theta\mathbf{u}_{\varphi}$

El sentido de la corriente depende de si el material es paramagnético o diamagnético, verificándose la regla de la mano derecha respecto al momento magnético inducido.

5 Casos particulares

Partícula magnética en un campo externo

De Laplace

Contenido

1 Enunciado

2 Magnetización y campo

3 Diamagnéticos y paramagnéticos

4 Corrientes de imanación

5 Casos particulares

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES