Despolarización de una esfera

De Laplace

Revisión a fecha de 18:31 17 mar 2009; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

Una esfera de radio $a$ se despolariza según la ley

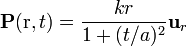
$\mathbf{P}(\mathrm{r},t)= \frac{k r}{1+(t/a)^2}\mathbf{u}_{r}$

Determine las densidades de carga de polarización, así como la densidad de corriente de polarización. ¿Se verifica la ley de conservación de la carga para $ρ p$ y $σ p$ ?

2 Solución

Las densidades de carga de polarización pueden ser de volumen o de superficie. En el primer caso

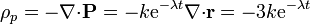
$\rho_p = -\nabla{\cdot}\mathbf{P} = -k\mathrm{e}^{-\lambda t}\nabla{\cdot}\mathbf{r} = -3k\mathrm{e}^{-\lambda t}$

en el interior de la esfera ($r<a$), mientras que en su exterior esta densidad es nula, ya que no hay polarización.

La carga de polarización almacenada en el volumen valdrá, por ser la densidad uniforme,

$Q_v = \int \rho_p \,d\tau = \left(\frac{4\pi}{3}a^3\right)\left(-3k\mathrm{e}^{-\lambda t}\right) = -4\pi a^3 k\mathrm{e}^{-\lambda t}$

Las densidades de carga superficiales se encontrarán en $r = a$

$\sigma_p = -\mathbf{n}{\cdot}[\mathbf{P}]= -\mathbf{u}_{r}{\cdot}\left(0-k\mathrm{e}^{-\lambda t}a\mathbf{u}_{r}\right)=k\mathrm{e}^{-\lambda t}a$

siendo la carga total almacenada en la superficie

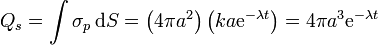
$Q_s =\int \sigma_p\,\mathrm{d}S =\left(4\pi a^2\right)\left(ka\mathrm{e}^{-\lambda t} \right)= 4\pi a^3 \mathrm{e}^{-\lambda t}$

Tanto la carga de volumen como la de superficie disminuyen en magnitud a lo largo del tiempo. La carga total de polarización será nula en todo instante

Q p = Q v + Q s = 0

La densidad de corriente de polarización valdrá en el interior de la esfera

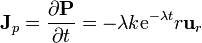
$\mathbf{J}_p = \frac{\partial{}\mathbf{P}}{\partial{}t} = -\lambda k \mathrm{e}^{-\lambda t} r\mathbf{u}_{r}$

y será nula en el exterior.

Esta densidad de corriente verifica la ley de conservación de la carga para $ρ p$ y para $σ p$ . En el primer caso tenemos

$\nabla{\cdot}\mathbf{J}_p = -3\lambda k\mathrm{e}^{-\lambda t}$

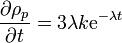
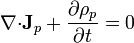
$\frac{\partial{}\rho_p}{\partial{}t} = 3\lambda k \mathrm{e}^{-\lambda t}$ $\nabla{\cdot}\mathbf{J}_p+\frac{\partial{}\rho_p}{\partial{}t}=0$

Para las superficiales empleamos la condición de salto

$\mathbf{n}{\cdot}[\mathbf{J}_p]= \mathbf{u}_{r}{\cdot}\left(0+\lambda k \mathrm{e}^{-\lambda t}a\mathbf{u}_{r}\right) = \lambda k a \mathrm{e}^{-\lambda t}$ $\frac{\partial{}\sigma_s}{\partial{}t} = -\lambda k a \mathrm{e}^{-\lambda t}\qquad \mathbf{n}{\cdot}[\mathbf{J}]=-\frac{\partial{}\sigma_s}{\partial{}t}$

Por supuesto, la ley de conservación de la carga puede demostrarse de forma general a partir de la definición de $ρ p$ , $σ p$ y 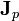$\mathbf{J}_p$

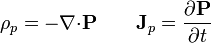
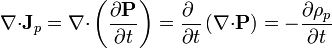
$\rho_p = -\nabla{\cdot}\mathbf{P} \qquad \mathbf{J}_p = \frac{\partial{}\mathbf{P}}{\partial{}t}$ $\nabla{\cdot}\mathbf{J}_p = \nabla{\cdot}\left(\frac{\partial{}\mathbf{P}}{\partial{}t}\right) = \frac{\partial{}\ }{\partial{}t}\left(\nabla{\cdot}\mathbf{P}\right)= -\frac{\partial{}\rho_p}{\partial{}t}$

y análogamente para las densidades de superficie

$\sigma_p = -\mathbf{n}{\cdot}[\mathbf{P}]$

$\mathbf{n}{\cdot}[\mathbf{J}_p] = \mathbf{n}{\cdot}\left[\frac{\partial{}\mathbf{P}}{\partial{}t}\right] = \frac{\partial{}\ }{\partial{}t}\left(\mathbf{n}{\cdot}[\mathbf{P}]\right)= -\frac{\partial{}\sigma_p}{\partial{}t}$

Despolarización de una esfera

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES