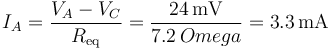Cinco resistencias iguales
De Laplace
Contenido |
1 Enunciado
Dado el sistema de resistencias de la figura, calcule la intensidad de corriente que entra por el extremo A en los siguientes casos:

-
 En A se conecta una fuente de 24mV, C se deja abierto y B se conecta a tierra.
En A se conecta una fuente de 24mV, C se deja abierto y B se conecta a tierra.
-
 En A se conecta una fuente de 24mV, B se deja abierto y C se conecta a tierra.
En A se conecta una fuente de 24mV, B se deja abierto y C se conecta a tierra.
-
 En A se conecta una fuente de 24mV, B y C se conectan a tierra.
En A se conecta una fuente de 24mV, B y C se conectan a tierra.
-
 En A se conecta una fuente de 24mV, en C una de 6mV y B se conecta a tierra.
En A se conecta una fuente de 24mV, en C una de 6mV y B se conecta a tierra.
-
 En A se conecta una fuente de 24mV, en B una de −24mV y C se conecta a tierra.
En A se conecta una fuente de 24mV, en B una de −24mV y C se conecta a tierra.
-
 En A se conecta una fuente de 24mV, en C una de −24mV y B se conecta a tierra.
En A se conecta una fuente de 24mV, en C una de −24mV y B se conecta a tierra.
2 Introducción
Este problema se puede resolver de forma general, dando como resultado una expresión matricial para las corrientes que entran por A, B y C en función de los voltajes de estos nodos. Más adelante se describe esta solución general, aplicable a todos los apartados del problema.
Aparte de este caso general, muchos casos particulares pueden simplificarse aplicando asociaciones en serie y en paralelo de resistencias.
3 Primer caso
En el primer caso, el nodo C está abierto, es decir, no tiene fuente conectada, por lo que por C no entra ni sale corriente.
En este caso, al ser todas las resistencias iguales y tener simetría, el voltaje en el nodo C será la media entre el del A y el B.
Lo mismo ocurre con el nodo D, que sería el superior.
Esto hace que entre C y D no haya diferencia de potencial y por tanto, por la rama central no circule corriente.
El sistema se reduce entonces a dos ramas en paralelo, ya que la resistencia central es como si no estuviera. La rama superior, pasando por D, tiene resistencia 2R, y la rama inferior, pasando por C, tiene también resistencia 2R, siendo 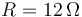 .
.
La resistencia equivalente del conjunto es

y por tanto la intensidad que entra por A (y sale por B) vale
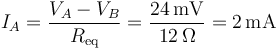
y, para los otros dos terminales
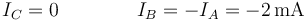
4 Segundo caso
En el segundo caso tenemos
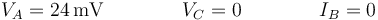
Este caso también se puede reducir a asociaciones en serie y en paralelo, aunque ya no hay simetría.
Para ir de A (entrada de la corriente) a C (salida de la corriente) hay dos caminos en paralelo. Uno va directo y tiene resistencia R. El otro va pasando por D y está formado por dos elementos en serie: una resistencia R y una asociación en paralelo de una resistencia R y una resistencia 2R. El esquema se puede reescribir de esta forma:

La resistencia equivalente de la rama superior es
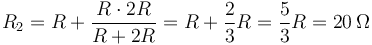
de manera que la resistencia equivalente del conjunto es
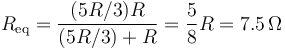
siendo la corriente que entra por A
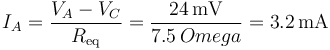
y, para los otros dos terminales

5 Tercer caso
Al poner los terminales B y C a tierra, estamos cortocircuitando la resistencia que entre estos dos nodos, ya que al estar al mismo potencial ya no circula corriente por ella.
Ahora el sistema se reduce a

(obsérvese que aunque B y C están en puntos distintos, entre ellos no hay resistencia alguna, por lo que están al mismo potencial)
La resistencia equivalente de la rama superior es ahora
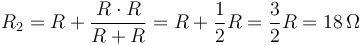
y la del conjunto
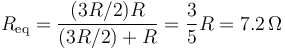
siendo la corriente que entra por A