Máquina de Atwood con resorte

De Laplace

1 Enunciado

Dos masas A y B, de masas 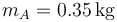y 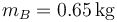están unidas por un hilo ideal (“1”), inextensible y sin masa, que pasa por una polea ideal, sin masa ni rozamiento. La masa A está unida al suelo por un resorte de constante 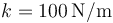y longitud natural 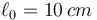. La B se mantiene a la misma altura que la primera mediante otro hilo ideal (“2”) de 15 cm de longitud. El sistema está inicialmente en equilibrio.

1. ¿Cuánto vale la tensión de cada hilo?
2. Suponga que se corta el hilo 2.
   1. ¿Cuánto vale la aceleración de cada masa justo tras el corte? ¿Y la tensión del hilo 1?
   2. ¿Cuánto mide la amplitud de las oscilaciones que describen las masas?
   3. ¿Cuál es la frecuencia ω de las oscilaciones que describe el sistema?
   4. Cuando el sistema está oscilando, ¿cuánto vale la tensión mínima del hilo? ¿Puede llegar a destensarse?

Tómese .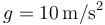

2 Tensiones

l equilibrio para la masa de la derecha da

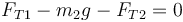
y para la de la izquierda

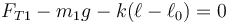
La fuerza elástica vale, teniendo en cuenta que el muelle mide 15cm

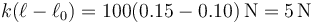
lo que da

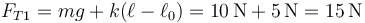
y

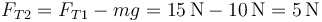
Dicho en palabras, para que estén en equilibrio a la misma altura, el hilo 2 debe hacer la misma fuerza que el muelle.