Onda en un hilo bimetálico
De Laplace
1 Enunciado
Un hilo de acero (ρ = 7.85 g/cm³) de 3.0 m y un hilo de cobre (ρ = 8.96 g/cm³) de 2.0 m ambos con un diámetro de 1 mm están conectados por un extremo. El extremo libre del acero está atado al techo, mientras que del del cobre cuelga una masa de 20 kg. ¿Cuánto tarda una oscilación de la masa en llegar hasta el techo?
- Sin tener en cuenta el incremento de tensión debido a la masa de los cables
- Teniendo en cuenta este incremento
2 Solución
2.1 Despreciando el peso de los cables
El tiempo en llegar al extremo superior es la suma del que emplea en recorrer el hilo de cobre más el que tarda en recorrer el de acero.
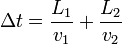
La velocidad en cada medio es diferente debido a las distintas densidades de masa. Para cada uno de los cables tenemos que
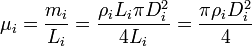
esto es, la densidad lineal de masa es igual a la masa total dividida por la longitud; la masa total es igual a la densidad volumétrica multiplicada por el volumen; el volumen es igual al producto de la sección (circular, con diámetro Di) por la misma longitud.
De aquí que la velocidad en cada medio sea
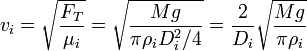
La tensión a la que están sometidos los dos cables es la misma e igual al peso de la masa situada en el extremo inferior. Esto presupone que despreciamos el efecto en la tensión de la masa de los propios cables. Más adelante examinaremos si este efecto es importante.
Sustituyendo en la expresión del tiempo de viaje nos queda finalmente






