Movimiento oscilatorio
De Laplace
Revisión a fecha de 01:04 6 mar 2009; Pedro (Discusión | contribuciones)
Contenido |
1 Movimiento oscilatorio
2 Movimiento armónico simple
3 Representación matemática del MAS: fase, periodo y frecuencia
4 Energía del MAS
5 Sistemas oscilantes: péndulo simple y péndulo físico
6 Oscilaciones amortiguadas y forzadas
6.1 Oscilaciones forzadas
Consideremos el caso de una masa m unida a un muelle de consntante recuperadora k y longitud natural nula,y sometida además a una fuerza de rozamiento proporcional a la velocidad. En este caso, las fuerzas que actúan sobre la masa son la fuerza recuperadora del muelle y la fuerza de rozamiento

El coeficiente b indica la intensidad de la fuerza del rozamiento. El signo negativo indica que esta fuerza se opone siempre a la velocidad.
Si suponemos que el movimiento se produce en una dimensión, escogiendo el eje X a lo largo de la dirección del movimiento podemos expresar las fuerzas como

El movimiento de la masa viene determinado por la Segunda Ley de Newton
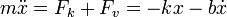
Reordenamos los términos de la ecuación y la escribimos
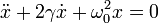
siendo

7 Problemas
Artículo completo: Problemas de movimiento oscilatorio





