Masa suspendida de un polipasto

De Laplace

1 Enunciado

Un bloque de masa m pende de un polipasto formado por dos poleas. La polea A tiene radio r y está unida rígidamente al bloque por una barra de longitud b. La polea B tiene el mismo radio y está fijada al techo por otra barra de longitud b. Un hilo inextensible sin masa está atado al techo, pasa por la polea A, luego por la B y está unida al bloque mediante un resorte de constante k y longitud natural 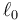. La longitud del hilo es tal que en ausencia de peso del bloque, el muelle estaría en su longitud natural y el hilo estirado pero sin tensión.

Se cuelga verticalmente el sistema.

1. Suponiendo que las poleas no tienen masa, halle la posición de equilibrio del bloque, h_eq, medida desde el techo. ¿Cuánto vale la tensión del hilo en ese estado?
2. Suponiendo que el bloque que se desplaza verticalmente una cantidad A respecto de la posición de equilibrio, determine la frecuencia de las oscilaciones que describe el bloque. ¿Cuánto debe ser el valor máximo de la amplitud si no se quiere que el hilo se destense?
3. Suponga ahora que las dos poleas son cilindros macizos de masa m₀, con su correspondiente momento de inercia. ¿Cuánto vale en ese caso la frecuencia de las oscilaciones?
4. Suponga ahora que el bloque está conectado a un amortiguador de constante γ ¿Cuál es la ecuación de movimiento del bloque en ese caso?

2 Posición de equilibrio

3 Frecuencia de las oscilaciones

4 Poleas no ideales

5 Oscilaciones amortiguadas