Motocicleta que acelera

De Laplace

Revisión a fecha de 18:52 10 ene 2018; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Cálculo de las fuerzas
3 Fuerzas sobre las ruedas
- 3.1 Rueda delantera
- 3.2 Rueda trasera
4 Aceleración máxima
5 Balance energético

1 Enunciado

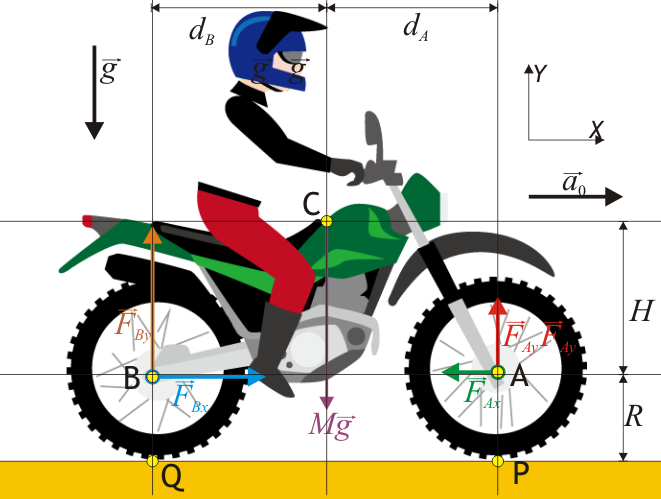
Es conocido que al arrancar un coche, éste levanta un poco el morro y se hunde por la parte trasera. El mismo principio se aplica a los caballitos de las motocicletas. Supongamos una motocicleta con una masa $M$ y tal que su centro de masas se encuentra a una altura $H$ respecto a los ejes de las ruedas (las cuales tienen radio $R$ , masa $m$ y momento de inercia $I$ ). El CM está a una distancia $d A$ del eje delantero y a una $d B$ del trasero.

Calcule la fuerza que se ejerce sobre cada eje cuando la moto arranca con una aceleración $a 0$ sobre un suelo horizontal.
Determine la fuerza de rozamiento que el suelo ejerce sobre cada rueda, así como el par ejercido por el motor sobre el eje de tracción (el de la rueda trasera).
¿Cuál es la aceleración máxima que puede alcanzar la moto sin que su rueda trasera patine?
¿Cuánto vale la potencia desarrollada por las diferentes fuerzas y momentos sobre el cuerpo y sobre las ruedas? ¿Cómo se transmite la energía aportada por el motor a las diferentes partes del sistema?

2 Cálculo de las fuerzas

Es evidente que al acelerar horizontalmente, se va a ejercer una fuerza horizontal sobre cada eje. Lo que ya no es tan evidente es que como resultado de esta aceleración se ejerza también una fuerza normal, que además es diferente sobre cada uno.

La razón es que a la hora de considerar el movimiento de un sólido, no solo hay que tener en cuenta la resultante de las fuerzas aplicadas, sino también las de los momentos.

Sobre el cuerpo o chasis de la moto se ejercen tres fuerzas:

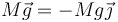
Su peso $M\vec{g}=-Mg\vec{\jmath}$
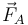
La fuerza que ejerce el eje delantero, $\vec{F}_A$
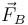
la fuerza que ejerce el eje trasero, $\vec{F}_B$

A su vez, las fuerzas ejercidas por los dos ejes se pueden descomponer en una componente vertical y una horizontal

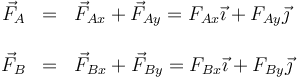
$\begin{array}{rcl}\vec{F}_A & = & \vec{F}_{Ax}+\vec{F}_{Ay} = F_{Ax}\vec{\imath}+F_{Ay}\vec{\jmath}\\ && \\ \vec{F}_B& =& \vec{F}_{Bx}+\vec{F}_{By} =F_{Bx}\vec{\imath}+F_{By}\vec{\jmath}\end{array}$

Al usar esta expresión no estamos presuponiendo el sentido de estas cuatro fuerzas, que aun son desconocidas. Solo asignamos una dirección. Cualquiera de las cuatro componentes puede ser negativa. De hecho, como veremos más adelante, una lo es.

El centro de masas (como el resto del cuerpo de la moto) adquiere una aceleración horizontal

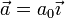
$\vec{a}=a_0\vec{\imath}$

por lo que la segunda ley de Newton nos da, para el balance de fuerzas sobre el sistema,

$\sum_i\vec{F}_i = M\vec{a}_C\qquad\Rightarrow\qquad \left\{\begin{array}{rcl} F_{Ax}+F_{Bx} & = & Ma_0 \\ -Mg+F_{Ay}+F_{By} & = & 0 \end{array}\right.$

Por otro lado, en la situación en que la moto no cabecea (suponemos una suspensión muy rígida), la suma de los momentos respecto al centro de masas debe anularse

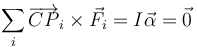
$\sum_i \overrightarrow{CP}_i\times\vec{F}_i=I\vec{\alpha}=\vec{0}$

De las cinco fuerzas que actúan sobre el sistema (considerando las de cada eje como dos, una horizontal y una vertical) el peso está aplicado sobre el propio CM, por lo que su momento es nulo. Los brazos de las otras cuatro son las distancias horizontales o verticales de sus rectas soporte al CM. De estas cuatro, tres producen un giro positivo y solo una negativo, de forma que tenemos

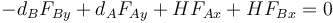
$-d_BF_{By}+d_AF_{Ay}+HF_{Ax}+HF_{Bx}=0\,$

Despejando y sustituyendo la ecuación para la aceleración del CM nos queda el sistema

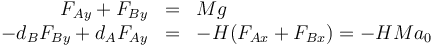
$\begin{array}{rcl} F_{Ay}+F_{By} & = & Mg \\ -d_BF_{By}+d_AF_{Ay} & = & -H(F_{Ax}+F_{Bx}) = -HMa_0 \end{array}$

con solución

$F_{Ay}= \frac{M(g d_B-a_0 H)}{d_A+d_B}\qquad\qquad F_{By}= \frac{M(g d_A+a_0 H)}{d_A+d_B}$

Vemos que para aceleración positiva, la fuerza que ejerce el eje delantero es menor que la del trasero (y por la tercera ley de Newton, lo mismo se cumplirá para la fuerza que la moto ejerce sobre los ejes). Esto es lo que provoca que una moto o un coche cabecee al acelerar, hundiéndose por la parte trasera.

Nótese que, con este cálculo, no podemos saber cuánto vale la fuerza horizontal sobre cada eje`por separado. Solo conocemos su suma. Para saber la fuerza individual debemos analizar qué pasa con cada rueda. La diferencia esencial es sobre cuál actúa el motor.

3 Fuerzas sobre las ruedas

Según el resultado anterior, el cuerpo de la motocicleta acelera hacia adelante porque desde los ejes se ejercen fuerzas hacia adelante.

Por la tercera ley de Newton, esto implica que la moto tira de sus ruedas hacia atrás. Pero si la moto, con su motor, tira de las ruedas hacia atrás, ¿cómo puede el vehículo avanzar aceleradamente?

La respuesta es que el que empuja a la moto hacia adelante no es el motor, sino el suelo. La fuerza externa que acelera el conjunto es la debida a la fricción estática con el suelo. Las ruedas empujan al suelo hacia atrás y, en reacción, el suelo empuja al coche hacia adelante. La fuerza total debida al rozamiento debe cumplir

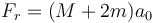
$F_r = (M+2m)a_0\,$

Pero incluso si admitimos esto tenemos un problema. Si el chasis tira de la rueda hacia atrás y el suelo empuja hacia adelante, se produce un par de fuerzas que haría girar la rueda hacia atrás (en sentido antihorario), cuando la evidencia es que gira hacia adelante (en sentido horario). ¿Cómo es posible?

La razón es que el motor no solo empuja o tira de las ruedas; también las hace girar. A través de la cadena unida al piñón produce un par de fuerzas que no acelera el CM de las ruedas (ya que la fuerza neta del par es nula) pero si genera rotación en el sentido correcto. Es de esta forma que el motor logra que al final sea el suelo el que empuje al vehículo.

3.1 Rueda delantera

Consideremos en primer lugar la rueda delantera, que no es una rueda motriz, es decir el motor no actúa sobre ella. Sobre esta rueda actúan las siguientes fuerzas:

El peso de la rueda, 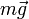$m\vec{g}$ , aplicado en su centro A.
La reacción normal del suelo, $\vec{F}_{Pn}$ , aplicada en el punto de contacto P.
El rozamiento con el suelo, 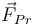$\vec{F}_{Pr}$ , que será del tipo estático y se aplica en el mismo punto P.
La fuerza vertical 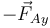$-\vec{F}_{Ay}$ , reacción de la calculada en el apartado anterior, que se aplica en A.
La fuerza horizontal, 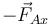$-\vec{F}_{Ax}$ , reacción de la mencionada (pero no calculada) en el apartado anterior, aplicada también en A.

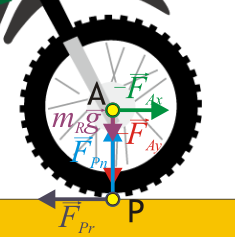
Separando por componentes nos quedan las relaciones

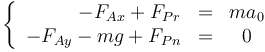
$\left\{\begin{array}{rlc} -F_{Ax}+F_{Pr} & = & ma_0 \\ -F_{Ay}-mg+F_{Pn} & = & 0\end{array}\right.$

Además tenemos la ecuación para el momento de las fuerzas respecto al centro de la rueda, tal como se ve en el apartado de la rodadura de una rueda

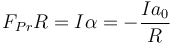
$F_{Pr}R = I\alpha = -\frac{Ia_0}{R}$

lo que nos permite relacionar la fuerza horizontal aplicada sobre esta rueda por el chasis

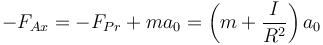
$-F_{Ax}= -F_{Pr}+m a_0 = \left(m+\frac{I}{R^2}\right)a_0$

Es decir, sobre esta rueda, no motriz, el chasis efectivamente empuja, y la rueda tira del chasis hacia atrás.

También hallamos la fuerza normal en el punto de contacto

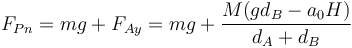
$F_{Pn} = mg + F_{Ay} = mg+\frac{M(g d_B-a_0 H)}{d_A+d_B}$

Si la aceleración es lo suficientemente grande puede anularse completamente la fuerza sobre el punto de contacto, y por tanto, levantar el vehículo por su morro. Esto es lo que consigue un motorista al hacer un caballito.

Para anular esta cantidad hay tres formas de conseguirlo, que se pueden aplicar simultáneamente: aumentar la aceleración, aumentar la altura del centro de masas, $H$ , y reducir la distancia al eje trasero, $d B$ . Esto lo consigue el motorista erguiéndose y echándose hacia atrás en la moto.

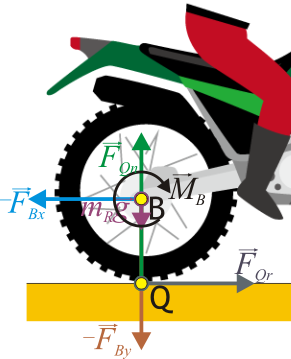
3.2 Rueda trasera

Para la rueda trasera realizamos un análisis similar

Puesto que la suma de las dos fuerzas horizontales de los ejes nos da la fuerza sobre el cuerpo de la moto

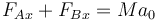
$F_{Ax}+F_{Bx} = Ma_0\,$

podemos hallar la fuerza entre el eje trasero y el chasis

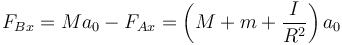
$F_{Bx} = Ma_0 - F_{Ax}= \left(M+m+\frac{I}{R^2}\right)a_0$

Esta es la fuerza que el eje trasero ejerce sobre el chasis, que es positiva. Por tanto, el eje trasero es el que empuja a la moto, la cual tira del eje hacia atrás.

Aplicando la segunda ley de Newton a la rueda trasera queda, si Q es su punto de contacto con el suelo

$\left\{\begin{array}{rlc} -F_{Bx}+F_{Qr} & = & ma_0 \\ -F_{By}-mg+F_{Qn} & = & 0\end{array}\right.$

De aquí obtenemos las componentes de la fuerza en el punto de contacto. La horizontal:

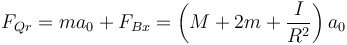
$F_{Qr} = ma_0 + F_{Bx} = \left(M+2m+\frac{I}{R^2}\right)a_0$

y la vertical

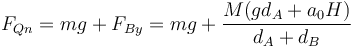
$F_{Qn} = mg + F_{By} = mg+\frac{M(g d_A+a_0 H)}{d_A+d_B}$

Sumando esta fuerza de rozamiento con la del eje delantero queda

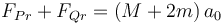
$F_{Pr}+F_{Qr} = \left(M+2m\right)a_0$

con lo que efectivamente, son las fuerza de rozamiento las que aceleran la moto y las ruedas hacia adelante.

Ahora bien, como dijimos antes, la fuerza $- F B x$ ejercida sobre el eje trasero y la fuerza de rozamiento $F Q r$ producen un par que tiende a hacer girar la rueda en sentido contrario al que se observa. Por ello, debe añadirse el par genera el motor sobre el eje (mediante una cadena y un piñón o por mecanismos más elaborados). Este par, aplicado en B, será en sentido de $-\vec{k}$ ya que tiende a girar la rueda en sentido horario. Por tanto tenemos

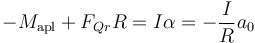
$-M_\mathrm{apl} +F_{Qr}R = I\alpha = -\frac{I}{R}a_0$

y queda finalmente

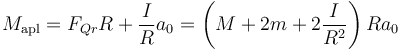
$M_\mathrm{apl} = F_{Qr}R+\frac{I}{R}a_0 = \left(M+2m+2\frac{I}{R^2}\right)Ra_0$

Este es el par que genera el motor y que es responsable de que la moto acelere, aunque sean las fuerzas de rozamiento las que realmente empujan.

4 Aceleración máxima

La condición para que la moto no patine al arrancar demasiado bruscamente la da el que no se supere el límite del rozamiento estático, para lo cual debe ser

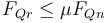
$F_{Qr}\leq \mu F_{Qn}$

Sustituyendo las dos componentes

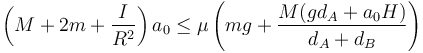
$\left(M+2m+\frac{I}{R^2}\right)a_0 \leq \mu\left(mg+\frac{M(g d_A+a_0 H)}{d_A+d_B}\right)$

Despejando de aquí obtenemos el máximo de $a 0$

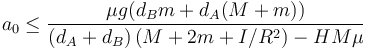
$a_0\leq \frac{\mu g (d_Bm+d_A (M+m))}{(d_A+d_B) \left(M+2m+I/R^2 \right)-H M \mu }$

5 Balance energético

Podemos hallar la potencia desarrollada por cada una de las fuerzas y ver cómo contribuye cada una a la variación de la energía cinética de cada parte del sistema.

5.1 Para el cuerpo

La potencia desarrollada sobre el cuerpo de la motocicleta será

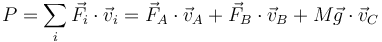
$P = \sum_i \vec{F}_i\cdot\vec{v}_i = \vec{F}_A\cdot\vec{v}_A+\vec{F}_B\cdot\vec{v}_B+M\vec{g}\cdot\vec{v}_C$

La potencia debida al peso es nula, ya que se trata de una fuerza vertical y la velocidad que adquiere la moto es horizontal. También se anulan las potencias de las fuerzas verticales ejercidas por los ejes, quedando solamente

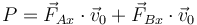
$P = \vec{F}_{Ax}\cdot\vec{v}_0+\vec{F}_{Bx}\cdot\vec{v}_0$

siendo $\vec{v}_0$ la velocidad de traslación del cuerpo, integral de la aceleración $\vec{a}_0$ que este adquiere.

Si sustituimos la suma de las dos fuerzas horizontales nos queda

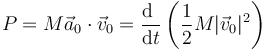
$P = M\vec{a}_0\cdot\vec{v}_0=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{1}{2}M|\vec{v}_0|^2\right)$

que no es más que el teorema trabajo-energía cinética: la potencia desarrollada por las fuerzas equivale a la derivada de la energía cinética del cuerpo.

Podemos desglosar la potencia realizada por cada una de las fuerzas. Para la del eje delantero

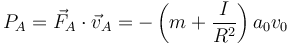
$P_A = \vec{F}_A\cdot\vec{v}_A = -\left(m+\frac{I}{R^2}\right)a_0v_0$

Esta potencia es negativa, lo que quiere decir que el eje delantero está extrayendo energía del sistema.

Para el eje trasero

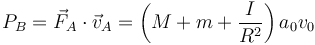
$P_B = \vec{F}_A\cdot\vec{v}_A = \left(M + m+\frac{I}{R^2}\right)a_0v_0$

es decir, el eje trasero aporta tanto la potencia que acelera el cuerpo como la que extrae el eje delantero.

5.2 Para la rueda delantera

Sobre la rueda delantera tenemos que

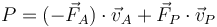
$P = (-\vec{F}_A)\cdot\vec{v}_A+\vec{F}_P\cdot\vec{v}_P$

(el signo menos para indicar que se trata de la fuerza de reacción de la calculada antes). La velocidad del punto P, de contacto de la rueda con el suelo, es nula, por lo que la potencia se reduce a

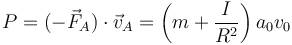
$P = (-\vec{F}_A)\cdot\vec{v}_A= \left(m+\frac{I}{R^2}\right)a_0v_0$

Esta es la opuesta a la calculada antes para el eje delantero, es decir, el eje extrae energía del cuerpo y se la comunica a la rueda.

Teniendo en cuenta que

$\omega = -\frac{v_0}{R}\qquad\qquad \alpha = -\frac{a_0}{R}$

esta potencia se puede escribir

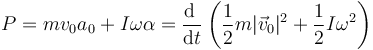
$P = m v_0a_0 + I \omega\alpha = \frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{1}{2}m|\vec{v}_0|^2+\frac{1}{2}I\omega^2\right)$

esto es, la fuerza ejercida por el eje sobre la rueda aumenta la energía cinética de traslación y la de rotación de la rueda (esto último con ayuda de la fuerza de rozamiento, que produce un par).

5.3 Para la rueda trasera

Sobre la rueda delantera debemos añadir la potencia debida al par ejercido por el motor

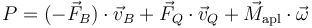
$P = (-\vec{F}_B)\cdot\vec{v}_B+\vec{F}_Q\cdot\vec{v}_Q+\vec{M}_\mathrm{apl}\cdot\vec{\omega}$

La velocidad del punto Q, de contacto de la rueda con el suelo, es nula.

La potencia debida a la fuerza ejercida por el eje es

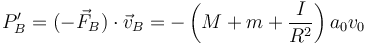
$P'_B = (-\vec{F}_B)\cdot\vec{v}_B= -\left(M+m+\frac{I}{R^2}\right)a_0v_0$

Esta potencia es negativa, es decir, se está extrayendo energía cinética de la rueda (que se comunica al cuerpo y através de este a la rueda delantera). ¿De donde sale? Del último término

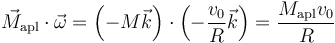
$\vec{M}_\mathrm{apl}\cdot\vec{\omega} = \left(-M\vec{k}\right)\cdot\left(-\frac{v_0}{R}\vec{k}\right) = \frac{M_\mathrm{apl}v_0}{R}$

Sustituimos el valor del par

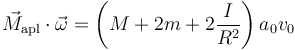
$\vec{M}_\mathrm{apl}\cdot\vec{\omega}=\left(M+2m+2\frac{I}{R^2}\right)a_0v_0$

que se puede desglosar como

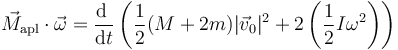
$\vec{M}_\mathrm{apl}\cdot\vec{\omega}=\frac{\mathrm{d}\ }{\mathrm{d}t}\left(\frac{1}{2}(M+2m)|\vec{v}_0|^2+2\left(\frac{1}{2}I\omega^2\right)\right)$

es decir, el motor proporciona tanto la energía cinética del cuerpo como la de las dos ruedas. Además al actuar sobre la rueda, el motor se la comunica a la rueda trasera, que parte la consume en sí misma, y parte la pasa al cuerpo, que a su vez transmite parte a la rueda delantera.

Motocicleta que acelera

De Laplace

Contenido

1 Enunciado

2 Cálculo de las fuerzas

3 Fuerzas sobre las ruedas

3.1 Rueda delantera

3.2 Rueda trasera

4 Aceleración máxima

5 Balance energético

5.1 Para el cuerpo

5.2 Para la rueda delantera

5.3 Para la rueda trasera

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES