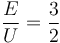Partícula en una superficie cónica (GIE)

De Laplace

Revisión a fecha de 18:31 27 nov 2017; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Enunciado
2 Rapidez
3 Fuerza de reacción
4 Proporción de energía
5 Expresión de cantidades

1 Enunciado

Una partícula de masa m se encuentra obligada a moverse sobre la superficie interior de un cono recto, de eje vertical y cuyo semiángulo en el vértice mide β. La partícula puede deslizar sin rozamiento sobre esta superficie y está sometido a la acción del peso, que va en la dirección vertical. Se desea que la partícula describa uniformemente circunferencias horizontales a una altura h respecto al vértice. Con ayuda de las coordenadas cilíndricas y la base asociada a ellas,

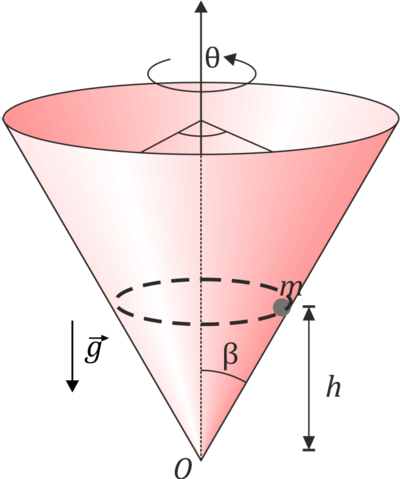
¿Qué rapidez $v 0$ debe comunicársele a la partícula, en función de la altura h?
¿Cuánto vale, en módulo, la reacción de la superficie cónica en este movimiento?
¿Cuánto vale la proporción E/U entre la energía mecánica y la potencial para este movimiento circular? Tómese como origen de energía potencial el vértice del cono.
Exprese, en la base de las coordenadas cilíndricas:
1. La cantidad de movimiento. ¿Es constante?
2. El momento cinético respecto a O. ¿Es constante?
3. La fuerza resultante sobre la partícula
4. El momento de las fuerzas sobre la partícula.

2 Rapidez

Este problema es, en lo esencial, idéntico al de la Masa girando alrededor de una mano y muy parecido al de curvas y peraltes

La partícula se mueve sometida a la acción de dos fuerzas: el peso

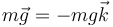
$m\vec{g}=-mg\vec{k}$

y la reacción de la superficie. Esta se calcula como en el caso de los problemas citados:

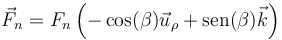
$\vec{F}_n=F_n\left(-\cos(\beta)\vec{u}_\rho+\mathrm{sen}(\beta)\vec{k}\right)$

Puesto que el movimiento es circular uniforme, la resultante de las dos fuerzas produce una aceleración puramente normal

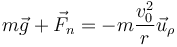
$m\vec{g}+\vec{F}_n=-m\frac{v_0^2}{r}\vec{u}_\rho$

siendo el radio de la circunferencia

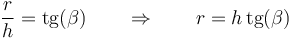
$\frac{r}{h}=\mathrm{tg}(\beta)\qquad\Rightarrow\qquad r = h\,\mathrm{tg}(\beta)$

Esto nos da

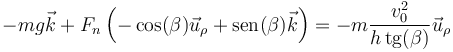
$-mg\vec{k}+F_n\left(-\cos(\beta)\vec{u}_\rho+\mathrm{sen}(\beta)\vec{k}\right)=-m\frac{v_0^2}{h\,\mathrm{tg}(\beta)}\vec{u}_\rho$

Separando por componentes, queda, en la dirección vertical

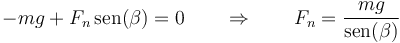
$-mg+F_n\,\mathrm{sen}(\beta)=0\qquad\Rightarrow\qquad F_n=\frac{mg}{\mathrm{sen}(\beta)}$

y en la radial

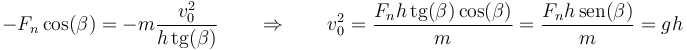
$-F_n\cos(\beta)=-m\frac{v_0^2}{h\,\mathrm{tg}(\beta)}\qquad\Rightarrow\qquad v_0^2=\frac{F_nh\,\mathrm{tg}(\beta)\cos(\beta)}{m}=\frac{F_nh\,\mathrm{sen}(\beta)}{m}=gh$

y por tanto la rapidez buscada es

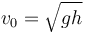
$v_0=\sqrt{gh}$

3 Fuerza de reacción

La fuerza de reacción, en módulo, ya la hemos calculado

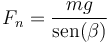
$F_n=\frac{mg}{\mathrm{sen}(\beta)}$

y, en forma vectorial

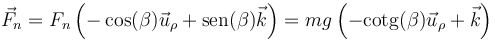
$\vec{F}_n=F_n\left(-\cos(\beta)\vec{u}_\rho+\mathrm{sen}(\beta)\vec{k}\right)=mg\left(-\mathrm{cotg}(\beta)\vec{u}_\rho+\vec{k}\right)$

4 Proporción de energía

La energía mecánica es la suma de la cinética y la potencial

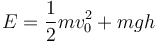
$E=\frac{1}{2}mv_0^2 + mgh$

Sustituimos el valor de la rapidez calculada antes

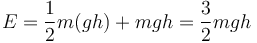
$E=\frac{1}{2}m(gh)+mgh=\frac{3}{2}mgh$

por lo que la proporción buscada es

$\frac{E}{U}=\frac{3}{2}$

5 Expresión de cantidades

5.1 Cantidad de movimiento

5.2 Momento cinético

5.3 Fuerza resultante

5.4 Momento de las fuerzas

Partícula en una superficie cónica (GIE)

De Laplace

Contenido

1 Enunciado

2 Rapidez

3 Fuerza de reacción

4 Proporción de energía

5 Expresión de cantidades

5.1 Cantidad de movimiento

5.2 Momento cinético

5.3 Fuerza resultante

5.4 Momento de las fuerzas

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES