Entrar Página Discusión Historial Go to the site toolbox

Potencia de un automóvil (GIE)

De Laplace

1 Enunciado

El rozamiento que experimenta un automóvil en movimiento rectilíneo depende de múltiples factores y en un determinado rango de velocidades entre 90 km/h y 130 km/h puede suponerse que la fuerza de rozamiento es lineal con la velocidad F = − (A + Bv). Supongamos un automóvil de 1500 kg que marcha por una carretera horizontal. Se conoce que la potencia que desarrolla para vencer la fricción es de 20 kW (26.8 CV) a 90 km/h y de 35 kW (46.9 CV) a 126 km/h

  1. Demuestre detalladamente que 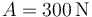A=300\,\mathrm{N} y que B=20\,\mathrm{kg}/\mathrm{s}.
  2. Supongamos que este coche debe ascender una pendiente del 6% (medida como la tangente del ángulo). ¿Qué potencia debe desarrollar a 90 km/h? ¿Y a 108 km/h?
  3. Si el coche desciende por una cierta pendiente del 6%, ¿a qué velocidad de descenso no es necesario ni acelerar ni frenar el coche?
  4. Supongamos que se acelera el coche uniformemente desde 90 km/h a 126 km/h empleando para ello una distancia de 500 m, ¿qué aceleración tiene el coche? ¿Cuánto es el trabajo total realizado sobre él en este incremento de velocidad? ¿Qué trabajo realiza el motor del coche en este incremento de velocidad?

Tómese 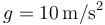g=10\,\mathrm{m}/\mathrm{s}^2

==Coeficientes==+ Tratando el vehículo como una partícula, la potencia que debe desarrollar en una superficie horizontal es la opuesta a la disipación por rozamiento

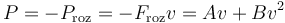
P=-P_\mathrm{roz}=-F_\mathrm{roz}v=A v + Bv^2\,

Sustituyendo los valores de las velocidades (en m/s) resulta el sistema

25A+{25}^2B=20000\qquad\qquad 35A+35^2B=35000

La solución de este sistema de dos ecuaciones con dos incógnitas da los valores del enunciado. Los valores de las fuerzas a estas dos velocidades son

F(25\,\mathrm{m}/\mathrm{s})=800\,\mathrm{N}\qquad\qquad F(35\,\mathrm{m}/\mathrm{s})=1000\,\mathrm{N}

variando linealmente en las velocidades intermedias.

2 Ascenso

En la subida, el coche debe vencer la potencia debida a la fricción y la debida a la componente tangencial del peso, que tira hacia abajo

P=(F_\mathrm{roz}+mg\,\mathrm{sen}(\beta))v= A v + B v^2 + (mg\,\mathrm{sen}(\beta))v

Para ángulos pequeños, el seno es prácticamente igual a la tangente, por lo que componente del peso es

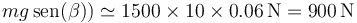
mg\,\mathrm{sen}(\beta))\simeq 1500\times 10\times 0.06\,\mathrm{N}=900\,\mathrm{N}

lo que nos da las potencias, a 90km/h (25m/s)

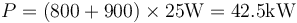
P=(800+900)\times 25\mathrm{W}=42.5\mathrm{kW}

y a 108km/h (30m/s)

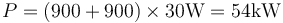
P=(900+900)\times 30\mathrm{W}=54\mathrm{kW}

3 Descenso

En la bajada, el peso ayuda el desplzamiento del automóvil. El coche no deberá acelerar ni frenar cuando se anule la suma la componente del peso, que empuja, con la la fricción, que se opone al movimiento.

mg\,\mathrm{sen}(\beta)-A-Bv=0\qquad\Rightarrow\qquad 900-300-20v=0\qquad\Rightarrow\qquad v = 30\,\frac{\mathrm{m}}{\mathrm{s}}=108\,\frac{\mathrm{km}}{\mathrm{h}}
Obtenido de "http://tesla.us.es/wiki/index.php/Potencia_de_un_autom%C3%B3vil_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace