Oscilador armónico bidimensional
De Laplace
Contenido |
1 Enunciado
Una partícula de masa m se encuentra sobre una mesa, unida a un punto fijo de ésta (que tomaremos como origen de coordenadas) mediante un muelle de constante k. En el instante t = 0 se la sitúa en la posición 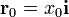 y se le comunica una velocidad
y se le comunica una velocidad 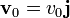 .
.
- Halle la posición de la partícula en cualquier instante.
- ¿Cómo es la trayectoria de la partícula?
- Demuestre que, en este movimiento, las cantidades
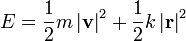
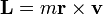
- son constantes de movimiento.
2 Solución
Aunque a la hora de pensar en osciladores armónicos, la visión más habitual es en términos de masas que se mueven en una sola dimensión, con un movimiento que varía sinusoidalmente en el tiempo, en realidad, un oscilador armónico no tiene por qué estar restringido a una sola dimension.
Lo que define al oscilador armónico, en general, es la ecuación de movimiento vectorial
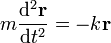
y sus soluciones describirán curvas tridimensionales.
2.1 Ley horaria
Para la partícula situada sobre la mesa, su movimiento será bidimensional y podrá describirse un sistema de coordenadas cartesiano
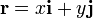
En este mismo sistema, la velocidad y la aceleración se escribirán
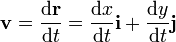
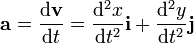
Sustituyendo en la ecuación de movimiento

y, puesto que dos vectores son iguales si lo son cada una de sus componentes, la ecuación vectorial se convierte en dos ecuaciones escalares
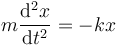
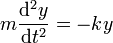
Esto quiere decir que el problema del oscilador armónico bidimensional (y el tridimensional) se puede reducir a dos osciladores armónicos unidimensionales (tres, en el tridimensional), cuya solución general es conocida:
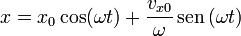

Combinando las dos soluciones obtenemos la solución general en forma vectorial
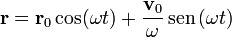
En nuestro caso, la posición inicial es


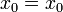
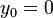
y la velocidad inicial