Barra oscilante sometida a una percusión horizontal
De Laplace
Contenido |
1 Enunciado
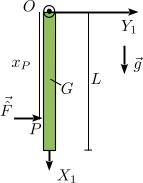
Una barra homogénea de longitud L está articulada en un punto fijo O de modo que puede colgar libremente, sometida a la acción de la gravedad. En el instante inicial se encuentra en reposo y colgando verticalmente. Se aplica un percusión horizontal hacia la derecha a una distancia xP del punto O. Determina la velocidad angular de la barra justo después de la percusión y las percusiones vinculares. Hazlo usando las herramientas de la Dinámica Vectorial y la Analítica.
2 Solución
2.1 Cinemática
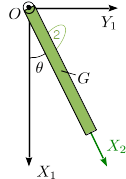
Resolvemos primero la cinemática del problema para poder describir el movimiento. Tenemos
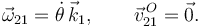
Tenemos un grado de libertad, la coordenada θ.
2.2 Dinámica vectorial
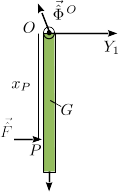
El vínculo en el punto O es que ese punto no se mueve. Al ser el problema plano, implica que hay dos componentes de percusión vincular que pueden ser no nulas. Las percusiones que actúan sobre la barra son
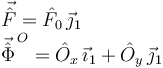
Tenemos tres incógnitas: 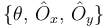 . === Dinámica vectorial ===
Tenemos que aplicar el T.C.M. impulsivo y el T.M.C. impulsivo.
. === Dinámica vectorial ===
Tenemos que aplicar el T.C.M. impulsivo y el T.M.C. impulsivo.
2.2.1 T.C.M.
Tenemos
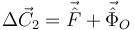
La gravedad no aparece en el proceso percusivo, pues es una fuerza de módulo acotado.
La cantidad de movimiento del centro de masas es
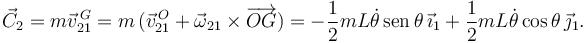
Durante la impulsión las coordenadas no cambian su valor. Además partimos del reposo. Por tanto tenemos
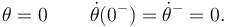
Entonces, la variación de la cantidad de movimiento es
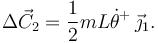
El T.C.M. impulsivo nos da dos ecuaciones escalares