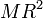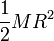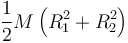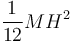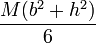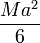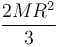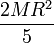Momento y tensor de inercia (CMR)
De Laplace
Contenido[ocultar] |
1 Definición
Dado un sólido rígido, se define su momento de inercia respecto a un eje como la cantidad
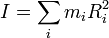
donde Ri es la distancia de una partícula m1 al eje. En el caso de que tengamos una distribución continua, la expresión correspondiente es la integral
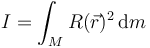
donde R será en general diferente para cada elemento de masa dm.
De la definición del momento de inercia se deduce que sus dimensiones son de una masa por una longitud al cuadrado y sus unidades en el SI son kg·m²
En los casos particulares frecuentes de que el eje respecto al que se calcula el momento de inercia se haga coincidir con uno de los ejes de coordenadas obtenemos los momentos de inercia
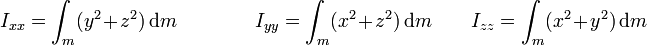
2 Ejemplos elementales
- Rotor equilibrado
- Consideremos un rotor formado por dos masas iguales de valor m situadas en los extremos de una varilla rígida ideal (sin masa) de longitud H con un eje de giro perpendicular a ella y que pasa por su centro. La distancia de cada masa al eje es la mitad de la longitud de la varilla, por lo que
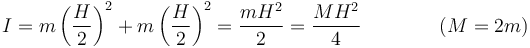
- Varilla homogénea
- Una barra de longitud H con una masa M distribuida uniformemente posee un momento de inercia respecto a un eje perpendicular a ella por su centro
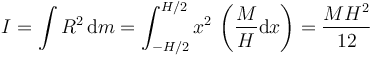
- donde hemos aplicado que por ser homogénea

- Superficie cilíndrica
- Para una superficie cilíndrica de radio R y altura h, el momento de inercia respecto al eje del cilindro es, simplemente
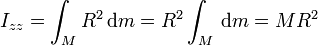
- ya que todos los puntos se encuentran a la misma distancia del eje.
- Cilindro macizo
- Si en cambio consideramos un cilindro macizo homogéneo de radio R y altura h, su momento de inercia es igual a
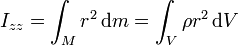
- Como elementos de volumen consideramos finas películas cilíndricas de radio r y espesor dr, cada una de las cuales tiene el volumen diferencial
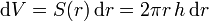
- Llevando esto al momento de inercia nos queda
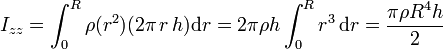
- Vemos que para cilindros del mismo material (con la misma densidad de masa), el momento de inercia va como la cuarta potencia del radio (esto es, doble de radio significa que el momento de inercia se multiplica por 16). Sustituyendo el valor de la densidad de masa
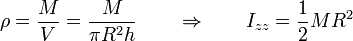
- El momento de inercia de un cilindro macizo es entonces la mitad del de una superficie cilíndrica de la misma masa y el mismo radio.
- Puesto que estos resultados no dependen de la altura del cilindro también son aplicables al caso de un anillo (superficie cilíndrica de altura muy pequeña) y de un disco (cilindro macizo de muy pequeño espesor).
3 Teorema de Steiner (o de los ejes paralelos)
El momento de inercia puede definirse respecto a un eje arbitrario, que no necesariamente debe pasar por el centro de masas del sólido. No obstante, los ejes que pasan por el CM tienen propiedades particulares.
Consideremos dos ejes paralelos: uno que pasa por el CM y uno situado a una distancia d del primero. Sea IG el momento de inercia respecto al eje que pasa por el CM e I el momento de inercia respecto al eje paralelo. Buscamos una relación entre estas dos cantidades.
Si consideramos el eje Z como el paralelo al que pasa por el CM el momento de inercia se puede escribir
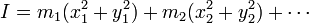
Introduciendo las posiciones relativas al CM
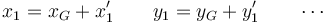
queda
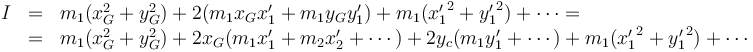
Ahora bien, la posición del centro de masas relativa a sí mismo es nula, por lo que

Además se cumple
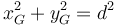
con d la distancia entre los ejes. Llevando esto a la expresión del momento de inercia queda
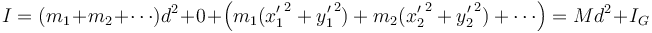
Este es el teorema de Steiner o de los ejes paralelos. Nos permite calcular el momento de inercia respecto a un eje arbitrario si conocemos el valor respecto a un eje paralelo que pase por el CM.
Este teorema nos dice que el momento de inercia en ejes paralelos es mínimo en el eje que pasa por el CM (lo cual sirve también como definición del centro de masas).
Por ejemplo, consideremos el momento de inercia de una varilla de masa M y longitud H alrededor de un eje que pasa por su extremo.
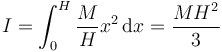
Si hallamos la diferencia con el que calculamos antes para el eje que pasa por el centro
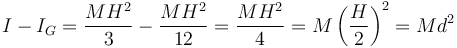
4 Teorema de la figura plana (o de los ejes perpendiculares)
Una sólido puede considerarse plano cuando sus dimensiones en una determinada dirección son mucho más pequeñas que a lo largo de las normales a ella. Es el caso, por ejemplo, de una chapa metálica en forma de disco o el de una varilla.
Si consideramos que la coordenada z es la que tiene espesor despreciable, podemos suponer que z = 0 para todos los puntos del sólido. Esto deja los tres momentos de inercia respecto a los ejes de coordenadas en
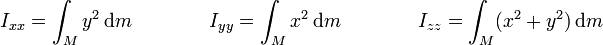
de donde es inmediato que
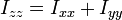
Esta relación permite calcular uno de los momentos de inercia conocidos los otros dos.
Por ejemplo, si deseamos hallar el momento de inercia de un disco circular respecto a un eje diametral podemos aplicar que, por simetría y por el teorema de la figura plana
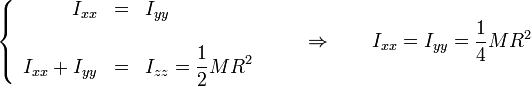
5 Casos particulares
Por su interés, es conveniente tabular casos particulares de momentos de inercia de sólidos homogéneos. Muchos otros pueden hallarse
Vemos que para aquellos que se caracterizan por una sola distancia R (radio, longitud,...), la forma del momento de inercia es
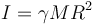
con γ un número que depende del objeto. En particular, para objetos redondos (con R el radio) tenemos
| Cuerpo | Cilindro hueco | Cilindro macizo | Esfera hueca | Esfera maciza |
|---|---|---|---|---|
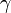
| 
| 
| 
| 
|
Esto permite estudiar de forma general los problemas de objetos rodantes, suponiendo un cierto factor γ general y luego particularizando.