Entrar Página Discusión Historial Go to the site toolbox

Caso de movimiento con aceleración constante (GIE)

De Laplace

Contenido

1 Enunciado

Una partícula se mueve con aceleración constante, de forma que en tres instantes sucesivos ocupa las siguientes posiciones

t(s) 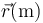\vec{r} (\mathrm{m})
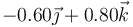
0\, -0.60\vec{\jmath}+0.80\vec{k}
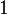
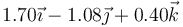
1\, 1.70\vec{\imath}-1.08\vec{\jmath}+0.40\vec{k}
2\, 4.80\vec{\imath}+2.28\vec{\jmath}+2.96\vec{k}
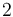
  1. Halle la velocidad media en el intervalo (0 s,2 s)
  2. Demuestre que la velocidad instantánea inicial (en t = 0\,\mathrm{s}) y la aceleración del movimiento valen

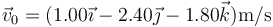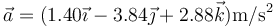
\vec{v}_0=(1.00\vec{\imath}-2.40\vec{\jmath}-1.80\vec{k})\mathrm{m}/\mathrm{s} y \vec{a}=(1.40\vec{\imath}-3.84\vec{\jmath}+2.88\vec{k})\mathrm{m}/\mathrm{s}^2

  1. Para el instante t = 1\,\mathrm{s}, halle:
    1. La velocidad, la rapidez y la aceleración instantáneas
    2. La aceleración tangencial y la aceleración normal (escalares)
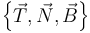
    3. Los vectores del triedro de Frenet \left\{\vec{T},\vec{N},\vec{B}\right\}
    4. El radio de curvatura y el centro de curvatura.

2 Velocidad media

La velocidad media en un intervalo es el vector

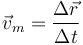
\vec{v}_m=\frac{\Delta\vec{r}}{\Delta t}

que en el intervalo (0s,2s) da

\vec{v}_m=\frac{\vec{r}_2-\vec{r}_0}{t_2-t_0}=\frac{\left(4.80\vec{\imath}+2.28\vec{\jmath}+2.96\vec{k}\right)-\left(-0.60\vec{\jmath}+0.80\vec{k}\right)}{2}=\left(2.40\vec{\imath}+1.44\vec{\jmath}+1.08\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}


3 Velocidad inicial y aceleración

4 Magnitudes en t = 1s

4.1 Velocidad, rapidez y aceleración

4.2 Componentes intrínsecas de la aceleración

4.3 Triedro de Frenet

4.4 Radio y centro de curvatura

Obtenido de "http://tesla.us.es/wiki/index.php/Caso_de_movimiento_con_aceleraci%C3%B3n_constante_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace