Cinemática de la partícula (CMR)
De Laplace
Contenido |
1 Introducción
La cinemática es la parte de la mecánica que estudia el movimiento sin atender a las causas que lo producen, es decir, de manera descriptiva.
La cinemática puede dividirse y particularizarse en estudios específicos atendiendo al tipo de movimiento (rectilíneo, plano, tridimensional,…) o al sistema que se trata (partícula, sistema de partículas, sólido, fluido,…)
Para ordenar esta materia, seguiremos el siguiente esquema:
- Un estudio general de la cinemática tridimensional de la partícula.
- La particularización de estas magnitudes al movimiento plano
- Una descripción de casos particulares importantes
Para bloques posteriores quedan:
- La cinemática del sólido rígido
- La cinemática del movimiento relativo
- El movimiento plano de sólidos
- La generalización en el contexto de la mecánica analítica.
2 Casos particulares
2.1 Movimiento uniforme
El movimiento de una partícula se dice uniforme cuando su rapidez es constante duante un cierto intervalo de tiempo

Esta definición es equivalente a que:
- La aceleración tangencial es nula durante todo ese intervalo.
- La aceleración es ortogonal a la velocidad en ese periodo de tiempo
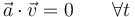
2.2 Movimiento rectilíneo
Un movimiento es rectilíneo en un intervalo de tiempo cuando su trayectoria en dicho intervalo es una recta. Esto ocurre si el vector tangente mantiene la misma dirección
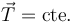
para ser precisos, puede invertir su sentido en instantes concretos, como ocurre en un movimiento armónico simple.
Esta condición equivale a que
- La aceleración normal es nula en dicho intervalo
- La aceleración es paralela a la velocidad
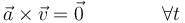
- La curvatura de la trayectoria es nula

- El radio de curvatura tiende a infinito.
Una manera de identificar un movimiento rectilíneo es comprobar si su ecuación horaria es de la forma
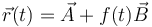
con  y
y  vectores constantes.
vectores constantes.
Si el movimiento es rectilíneo y uniforme, la velocidad de la partícula es constante

o, dicho de otra forma, si la aceleración tangencial y la normal son ambas nulas, el vector aceleración es nulo.
2.3 Movimiento plano
Movimiento plano de una partícula es aquel que en todo momento de un intervalo se encuentra contenido en un plano. Si A es un punto de este plano y  es un vector normal a él, debe cumplirse la ecuación vectorial
es un vector normal a él, debe cumplirse la ecuación vectorial
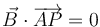
o, empleando los vectores de posición
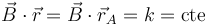
Alternativamente, un movimiento es plano si puede escribirse en la forma
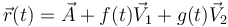
con  ,
, 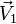 y
y 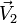 vectores constantes.
vectores constantes.
2.4 Movimiento circular
Un movimiento circular es aquel cuya trayectoria es una circunferencia. Esto implica que
- El movimiento es plano: Existe un vector constante
 tal que
tal que
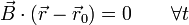
- El radio de curvatura permanece constante:

Estas dos condiciones pueden reducirse a una sola:
- El centro de curvatura permanece constante:
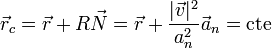
Por tanto, dadas la ecuación horaria del movimiento o, más en general, la trayectoria en función de cualquier parámetro, si calculamos el centro de curvatura y resulta un vector constante el movimiento es circular, aunque en la expresión no sea evidente.
2.4.1 Velocidad angular
En cualquier movimiento, se verifica en todo instante que
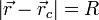
en el caso particular de un movimiento circular R y  son constantes, por lo que si elevamos al cuadrado esta expresión
son constantes, por lo que si elevamos al cuadrado esta expresión
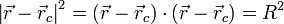
y derivamos respecto al tiempo
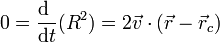
esto es, la velocidad es siempre perpendicular al vector de posición relativa al centro de la circunferencia. Esta ortogonalidad permite escribir la velocidad como
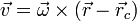
donde  es la velocidad angular. Es un vector perpendicular al plano de la trayectoria circular y con un sentido tal que se verifica la regla de la mano derecha respecto al giro (si los dedos de la mano derecha apuntan en la dirección del giro, el pulgar marca la dirección y sentido de la velocidad angular).
es la velocidad angular. Es un vector perpendicular al plano de la trayectoria circular y con un sentido tal que se verifica la regla de la mano derecha respecto al giro (si los dedos de la mano derecha apuntan en la dirección del giro, el pulgar marca la dirección y sentido de la velocidad angular).
La velocidad angular posee dimensiones de 1/tiempo, con lo que en el sistema internacional se mide en s-1 o rad/s.
2.4.2 Aceleración angular
Derivando en la expresión anterior para la velocidad
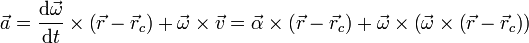
El vector

es la aceleración angular del movimiento. En el sistema internacional, sus unidades son rad/s².
2.4.3 Movimiento circular uniforme
El movimiento circular uniforme es el que ocurre a celeridad constante

En este movimiento la velocidad no es constante, puesto que su dirección está cambiado. La aceleración es puramente normal
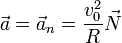
lo que implica que la aceleración va en la dirección de la posición relativa al centro de la circunferencia, y dirigida hacia adentro y puesto que estos dos vectores son de módulo constante se cumple
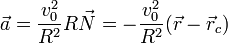
En un movimiento circular uniforme la velocidad angular es constante
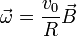
siendo  el vector normal al plano de la circunferencia. La aceleración angular es nula
el vector normal al plano de la circunferencia. La aceleración angular es nula
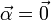
La aceleración puede escribirse en términos de la velocidad angular como

Un movimiento circular uniforme es periódico, siendo el periodo de revolución el tiempo necesario para dar una vuelta completa
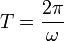
Al número de vueltas que la partícula da por segundo se le denomina la frecuencia natural
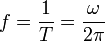
2.4.4 Movimiento en el plano XY
Puesto que los sistemas de referencia son arbitrarios, una vez que sabemos que un movimiento es circular, podemos tomar el origen de coordenadas en el centro de la circunferencia y los ejes de forma que la trayectoria esté contenida en el plano XY y con el origen de coordenadas en el centro de la circunferencia. En coordenadas polares, una circunferencia centrada en el origen se escribe simplemente

La ecuación vectorial de la trayectoria se reduce a

siendo la ley horaria
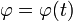
La velocidad de un movimiento circular es puramente acimutal,
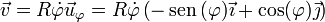
siendo la rapidez y el vector tangente

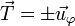
El signo variable depende del sentido de recorrido sobre la circunferencia. Por ejemplo, el movimiento de la lenteja de un péndulo es circular (aunque no complete una circunferencia) pero en su vaivén, el vector tangente unas veces coincide con el unitario en la dirección acimutal y otras es el opuesto.
La distancia medida sobre la curva



La velocidad angular va en la dirección normal al plano y es tal que al multiplicarla vectorialmente por  resulta la velocidad. Esto da
resulta la velocidad. Esto da

La aceleración de la partícula es
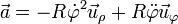
con componentes intrínsecas
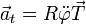

con el vector normal
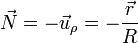
Por último, la aceleración angular viene dada por
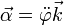
Con estos ejes, un movimiento circular uniforme corresponde a
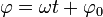
con ω constante.






