Dinámica de la partícula no vinculada (CMR)
De Laplace
Contenido |
1 Definición
Una partícula no vinculada es aquella que puede moverse sin obstáculo en las tres direcciones del espacio, aunque puede estar sometida a fuerzas que afectan a su movimiento.
El que pueda describir tres movimientos independientes, y por tanto para especificar su posición se requieran tres coordenadas se expresa diciendo que la partícula tiene 3 grados de libertad.
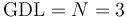
El número de grados de libertad se expresa como GDL o D.O.F. (degrees of freedom).
2 El problema fundamental de la dinámica
En esencia, el problema que se plantea al estudiar la partícula no vinculada es ¿cómo se mueve esto? Es decir, se conoce el estado inicial (posición y velocidad) de la partícula y se conocen las fuerzas que actúan sobre ella (a partir de alguna ley de fuerza: gravitación, electromagnetismo, fuerzas elásticas,…) y a partir de ahí se trata de determinar su posición en un instante posterior.
Matemáticamente se trata de plantear la ecuación de movimiento
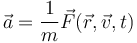
con las condiciones iniciales

Obsérvese que suponemos que la fuerza depende de la posición, la velocidad y el tiempo, pero no de la propia aceleración. Eso es una evidencia física. Cuando se suponen fuerzas dependientes de la aceleración se obtienen resultados físicamente absurdos.
Desde el punto de vista del cálculo es más útil escribir la ecuación de movimiento como ecuaciones diferenciales de primer orden, con lo que queda
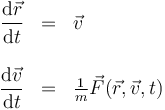
con las condiciones iniciales

Considerando que cada vector tiene tres componentes, esto son seis ecuaciones diferenciales de primer orden acopladas (es decir, que no se pueden resolver independientemente, ya que la solución de cada una depende de las demás).
Hay ocasiones en que la solución es trivial (caso de una fuerza constante), en otras existen soluciones analíticas más o menos complejas, pero en muchos casos, la solución de las ecuaciones de movimiento requiere el cálculo numérico.





