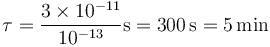Corrientes de intensidad variable (GIE)

De Laplace

Revisión a fecha de 16:25 23 abr 2016; Antonio (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

Contenido

1 Introducción
2 El condensador real
3 Descarga de un condensador
4 Carga de un condensador
5 Corriente alterna

1 Introducción

En general, el movimiento de las cargas es una función del tiempo. No obstante, es de especial interés el caso estacionario (que no estático) en el cual las cargas se mueven pero en un determinado punto del sistema siempre tienen la misma velocidad promedio, de manera que la densidad de corriente es siempre la misma. En ese caso se dice que tenemos corriente continua.

En corriente continua todas las derivadas respecto al tiempo son nulas. En particular, la carga de un condensador permanecerá constante.

Cuando el movimiento de las cargas es función del tiempo hay que tener en cuenta efectos como la variación de la carga en los condensadores y la inducción electromagnética.

El caso general de corrientes dependientes del tiempo puede ser extremadamente complicado, ya que aparecen fenómenos como la radiación electromagnética o el acoplamiento entre diferentes partes de un circuito.

Aquí consideraremos los casos más sencillos. Supondremos corrientes variables en el tiempo pero que cambian lentamente. En este caso, pueden aplicarse generalizaciones de las fórmulas de corriente continua (en particular, la ley de Ohm y la relación entre carga y potencial de un condensador) pero admitiendo que $I = I (t)$ .

2 El condensador real

En su forma general, la ley de conservación de la carga nos dice que la carga ni se crea ni se destruye. Esto quiere decir que si en un volumen cerrado la cantidad de carga contenida está disminuyendo es porque está escapando al exterior (ya que no puede desaparecer).

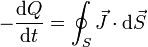
$-\frac{\mathrm{d}Q}{\mathrm{d}t}=\oint_S \vec{J}\cdot\mathrm{d}\vec{S}$

Consideremos ahora el caso de un condensador real, o condensador con pérdidas, formado por dos placas metálicas altamente conductoras, entre las cuales se encuentra un medio material dieléctrico de permitividad $\varepsilon$ que tiene una pequeña conductividad $σ$ . En este caso el condensador no funciona como un circuito abierto, sino que puede haber una corriente óhmica que lo atraviese.

Sea $I$ la intensidad de corriente que llega a la placa positiva del condensador. Esa corriente no tiene por qué igualar a la que atraviesa el condensador, ya que puede haber variación en la carga almacenada.

Sea S una superficie cerrada que envuelve a la placa positiva. Aplicando la ley de conservación de la carga a esta superficie queda

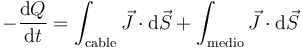
$-\frac{\mathrm{d}Q}{\mathrm{d}t}=\int_\mathrm{cable} \vec{J}\cdot\mathrm{d}\vec{S}+\int_\mathrm{medio} \vec{J}\cdot\mathrm{d}\vec{S}$

La integral a través de la sección del cable es igual a la intensidad de corriente cambiada de signo, ya que hemos definido I como la corriente que entra, no la que sale

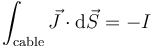
$\int_\mathrm{cable} \vec{J}\cdot\mathrm{d}\vec{S} = -I$

Sustituimos y despejamos y queda

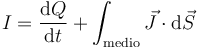
$I = \frac{\mathrm{d}Q}{\mathrm{d}t}+\int_\mathrm{medio} \vec{J}\cdot\mathrm{d}\vec{S}$

que podemos leer como que la intensidad de corriente que llega parte se emplea en variar la carga almacenada y parte se escapa por el medio dieléctrico.

Tenemos tres casos particulares:

Dieléctrico ideal: si el medio dieléctrico no tiene conductividad, la densidad de corriente en él es nula y la ecuación anterior se reduce a

$I = \frac{\mathrm{d}Q}{\mathrm{d}t}\qquad\qquad (\vec{J}=\vec{0})$

Éste es el único caso en que la intensidad de corriente es igual a la derivada de la carga respecto al tiempo, cuando tenemos un condensador ideal de resistencia infinita (o conductancia nula).

Caso estacionario: Si estamos en una situación de corriente continua, todas las derivadas respecto al tiempo se anulan y queda

$I = \int_\mathrm{medio} \vec{J}\cdot\mathrm{d}\vec{S}\qquad\qquad \left(\frac{\mathrm{d}Q}{\mathrm{d}t}=0\right)$

En este caso, toda la corriente que llega sigue circulando por el material y el dispositivo se comporta como una resistencia. Esto no quiere decir que no haya carga en las placas, sino que ésta es constante en el tiempo. Ahora bien, si la carga puede circular por el material, ¿cómo puede quedarse a la vez quieta en las placas? La respuesta es que las cargas individuales que están en las placas no son siempre las mismas. Un electrón llega a la placa negativa y las fuerzas eléctricas tiran de él y lo hacen atravesar el material, pero como las placas están conectadas a un generador, las cargas que escapan son sustituidas por otras nuevas.

Dispositivo aislado: Si desconectamos el generador se anula la intensidad de corriente que llega por el cable y la ecuación se reduce a

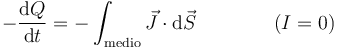
$-\frac{\mathrm{d}Q}{\mathrm{d}t}=-\int_\mathrm{medio} \vec{J}\cdot\mathrm{d}\vec{S}\qquad \qquad (I=0)$

En este caso lo que tenemos es que sin aporte externo de carga las placas se descargan gradualmente porque se escapan por el material.

Si la carga y la corriente en un condensador real varían lentamente con el tiempo, puede suponerse que la carga es proporcional a la diferencia de potencial, como en el caso estático

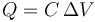
$Q=C\,\Delta V$

mientras que la corriente que circula por el material verifica la ley de Ohm, por tratarse de un material con conductividad

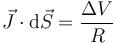
$\vec{J}\cdot\mathrm{d}\vec{S}=\frac{\Delta V}{R}$

En el caso particular de un condensador de placas paralelas, esta capacidad y resistencia valen

$C = \frac{\varepsilon S}{a}\qquad\qquad R=\frac{a}{\sigma S}$

Con estas relaciones, la intensidad de corriente que llega al condensador con pérdidas se expresa

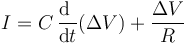
$I=C\,\frac{\mathrm{d}\ }{\mathrm{d}t}(\Delta V)+\frac{\Delta V}{R}$

Si el condensador es ideal (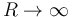 $R\to\infty$ ) la corriente se reduce a

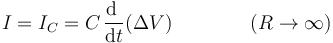
$I=I_C=C\,\frac{\mathrm{d}\ }{\mathrm{d}t}(\Delta V)\qquad\qquad (R\to\infty)$

y si la corriente es continua se anula la derivada respecto al tiempo

$I=I_R=\frac{\Delta V}{R}\qquad\qquad\left(\frac{\mathrm{d}\ }{\mathrm{d}t}(\Delta V)=0\right)$

En el caso general tendremos la suma de los dos términos

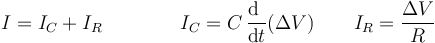
$I=I_C+I_R \qquad\qquad I_C=C\,\frac{\mathrm{d}\ }{\mathrm{d}t}(\Delta V)\qquad I_R=\frac{\Delta V}{R}$

En términos de un circuito equivalente, el que la corriente que llega se escriba como suma de dos contribuciones nos dice que se puede modelar como dos elementos en paralelo. Uno de ellos es un condensador ideal, de resistencia infinita, y la corriente que pasa por él se denomina corriente capacitiva. El segundo es un resistor óhmico, sin capacidad, y la corriente que lo atraviesa es la componente resistiva.

En corriente continua solo pasa corriente por la resistencia, pero en situaciones de corrientes variables en el tiempo también hay componente capacitiva (lo que quiere decir en realidad que está variando la carga almacenada).

3 Descarga de un condensador

Como ejemplo de corriente variable tenemos el caso de la descarga de un condensador con pérdidas.

Supongamos en primer lugar que el condensador está conectado a una fuente de tensión contínua $V 0$ . En ese caso la carga almacenada en el condensador permanece constante e igual a $C V 0$ . Simultáneamente, por el dieléctrico fluye una corriente $V 0 / R$ . Como se comentó antes, las cargas individuales que se encuentran en las placas no son siempre las mismas, sino que atraviesan el material y son sustituidas por nuevas cargas procedentes del generador.

Si ahora desconectamos el generador, cesa el aporte de cargas externas y las que fluyen por el material no son repuestas. Como resultado, el condensador se descarga progresivamente.

Matemáticamente lo que tenemos es la ecuación diferencial

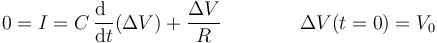
$0 = I = C\,\frac{\mathrm{d}\ }{\mathrm{d}t}(\Delta V)+\frac{\Delta V}{R}\qquad\qquad \Delta V(t=0)=V_0$

o, equivalentemente

$\frac{\mathrm{d}\ }{\mathrm{d}t}(\Delta V)=-\frac{1}{RC}\Delta V\qquad\qquad \Delta V(t=0)=V_0$

La solución de esta ecuación diferencial es una exponencial decreciente

$\Delta V = V_0 \mathrm{e}^{-t/\tau}\qquad\qquad \tau = RC$

La constante de tiempo τ = RC es el llamado tiempo de carga (o de descarga, en este caso) del condensador. Da una medida del tiempo que tarda en descargarse el condensador, aunque este realmente requeriría un tiempo infinito, pasado 2 o 3 veces τ ya se puede suponer que está descargado.

En el caso de un condensador plano lleno de un medio dieléctrico con conductividad

$RC = \frac{a}{\sigma S}\,\frac{\varepsilon S}{a}=\frac{\varepsilon}{\sigma}$

Este tiempo suele ser muy breve salvo en dieléctricos muy muy aislantes. Por ejemplo, para el metacrilato, la conductividad es de $10 - 13 S / m$ y la permitividad es 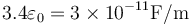$3.4\varepsilon_0 = 3\times 10^{-11}\mathrm{F}/\mathrm{m}$ lo que da una constante de tiempo

$\tau = \frac{3\times 10^{-11}}{10^{-13}}\mathrm{s}=300\,\mathrm{s}=5\,\mathrm{min}$

4 Carga de un condensador

5 Corriente alterna

Corrientes de intensidad variable (GIE)

De Laplace

Contenido

1 Introducción

2 El condensador real

3 Descarga de un condensador

4 Carga de un condensador

5 Corriente alterna

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES