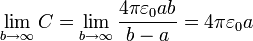Condensador esférico
De Laplace
Contenido |
1 Enunciado
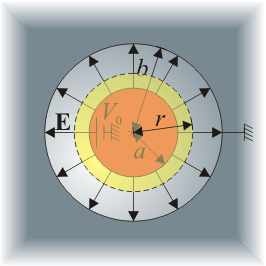
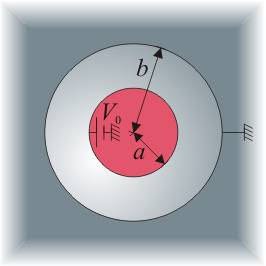
Halle la capacidad de un condensador formado por dos superficies esféricas concéntricas, de radios a y b (a < b).
2 Solución
2.1 Caso general
Suponemos la superficie interior a potencial V0 y la exterior a tierra.
En el hueco entre las dos superficies esféricas no hay carga intermedia, por lo que se verifica la ecuación de Laplace

con las condiciones de contorno
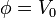

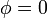
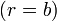
Por la simetría del sistema, podemos suponer que el potencial depende exclusivamente de la coordenada radial r. En este caso, la solución de la ecuación de Laplace es de la forma

Quedan por determinar las constantes A y B. Sustituyendo las condiciones de contorno
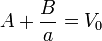
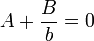
resultan las constantes y el potencial
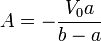
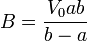
y sustituyendo las constantes en la expresión del potencial
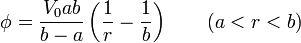
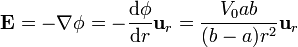
La carga en la esfera a mayor potencial (la interior) la calculamos por aplicación de la ley de Gauss. Si tomamos una superficie esférica de radio r concéntrica con la esfera interior
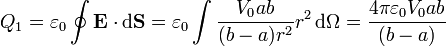
ya que para una superficie esférica 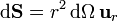 y el ángulo sólido total Ω = 4π.
y el ángulo sólido total Ω = 4π.
La capacidad del condensador esférico la obtenemos como el cociente entre la carga y la diferencia de potencial
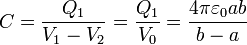
2.2 El límite de radio exterior infinito
Un límite de interés del resultado anterior es el límite en que 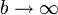 . En este límite
. En este límite