Variación de la presión de los neumáticos
De Laplace
Contenido |
1 Enunciado
Un automovilista llena los neumáticos de su coche a una presión manométrica de 2.4 bar un día de enero en que la temperatura exterior es de 5°C. Si no los toca en seis meses y no hay fugas, ¿cuál será la presión manométrica un día de julio a 40°C? ¿Qué proporción de aire debe extraer de cada neumático para devolver la presión a 2.4 bar? Si tras reducir la presión se despreocupa otros seis meses, ¿cuál será la presión manométrica cuando vuelva a hacer 5°C? Desprecie la dilatación de los neumáticos.
2 Presión en verano
Si despreciamos la dilatación de los neumáticos se trata de un proceso de calentamiento a volumen constante, para el cual se cumple
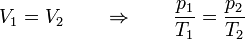
En el estado inicial la temperatura 5°C y la presión manométrica es de 2.4 bares. La presión absoluta será ésta, más la atmosférica, que es aproximadamente 1 bar (una atmósfera estándar son en realidad 1,013 bares, pero teniendo en cuenta que se nos da la presión manométrica con solo dos cifras significativas, no hace falta introducir más decimales).

En el estado final, en verano, la temperatura ha aumentado
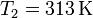
Esto nos da la presión absoluta en verano
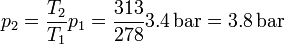
y la manométrica
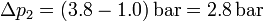
3 Desalojo de gas
Para aliviar la presión sobre los neumáticos, es preciso dejar salir una parte del gas. La cantidad de gas que debe salir lo hallamos como la diferencia entre la masa que hay actualmente y los que debería haber para que a esta temperatura y con este volumen si la presión manométrica se redujera a 2.4 bares. Sin desinflar, en los neumáticos hay una masa
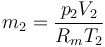
siendo Rm la constante del gas (aire, en este caso). Es preferible emplear esta fórmula en vez de la de la constante universal, por ser el aire una mezcla, en vez de una sustancia pura. Como veremos, eso no afecta al resultado.
Tras vaciar el neumático, debe ser

donde
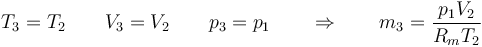
(solo cambia la presión respecto a la fórmula anterior). El cociente entre ambas cantidades nos permite librarnos del volumen, que no conocemos,

Si lo que nos interesa es la fracción que hay que vaciar, debemos dividir la diferencia entre la cantidad de gas que había antes y la que hay después por la cantidad de gas que había antes de vaciar el neumático,
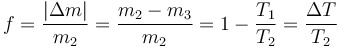
que numéricamente nos da
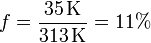
4 Presión en invierno
Una vez que se vuelve a enfriar, la presión se reduce, manteniéndose constante el volumen. De nuevo se cumple

donde
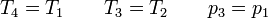
lo que nos da la presión absoluta

y la barométrica
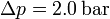
Vemos, por tanto, que hay cambios sustanciales en la presión de los neumáticos simplemente por el cambio estacional.





