5.9. Silla giratoria (Ex.Dic/12)

De Laplace

Revisión a fecha de 14:51 20 dic 2012; Enrique (Discusión | contribuciones)

(dif) ← Revisión anterior | Revisión actual (dif) | Revisión siguiente → (dif)

1 Enunciado

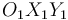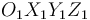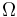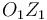Una placa cuadrada (sólido "0") de lado $L\,$ , que se mantiene en todo instante en un plano horizontal paralelo al plano $O_1X_1Y_1\,$ del triedro fijo $O_1X_1Y_1Z_1\,$ (sólido "1"), está rotando con velocidad angular constante $\Omega\,$ (en el sentido indicado en la figura) alrededor del eje vertical fijo que pasa por su centro $O\,$ (eje $O_1Z_1\,$ ). A su vez, una placa rectangular ABCD (sólido "2"), de dimensiones 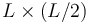$L\times(L/2)\,$ y vinculada a la placa cuadrada mediante un par de bisagras en su lado AB, está rotando con velocidad angular constante 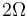$2\Omega\,$ (en el sentido indicado en la figura) respecto a la placa cuadrada.

Expresando las magnitudes vectoriales en la base asociada al triedro 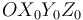$OX_0Y_0Z_0\,$ de la figura, el cual se mueve solidariamente con la placa cuadrada "0", determine:

Reducción cinemática canónica de los movimientos {01} y {20}.
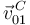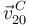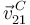Velocidades $\vec{v}^{\, C}_{01}\,$ , $\vec{v}^{\, C}_{20}\,$ y $\vec{v}^{\, C}_{21}\,$ para el instante particular representado en la figura, el cual corresponde a la placa rectangular ABCD en posición vertical por encima de la placa cuadrada.
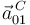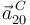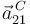Aceleraciones $\vec{a}^{\, C}_{01}\,$ , $\vec{a}^{\, C}_{20}\,$ y $\vec{a}^{\, C}_{21}\,$ para el mismo instante del apartado anterior.

2 Reducciones cinemáticas canónicas {01} y {20}

De la lectura del enunciado, se deduce que tanto el movimiento {01} como el movimiento {20} son rotaciones puras alrededor de ejes fijos (ejes permanentes de rotación). En concreto, el EPR{01} es el eje 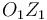$O_1Z_1\,$ , y el EPR{20} es el eje 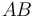$AB\,$ . Según la terminología propia de los pares cinemáticos, cabe decir que {01} y {20} constituyen sendos pares de revolución.

Sabemos que la reducción cinemática de un movimiento en un punto es el conjunto formado por el vector velocidad angular (invariante) y el vector velocidad de dicho punto. Y se denomina canónica a la reducción cinemática realizada en un punto del eje central. En el caso presente, vamos a elegir el punto 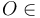$O\in\,$ EPR{01} para la reducción cinemática canónica del movimiento {01}, y el punto 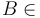$B\in\,$ EPR{20} para la reducción cinemática canónica del movimiento {20}. Las correspondientes velocidades de estos puntos (la {01} de $O\,$ y la {20} de $B\,$ ) son nulas por tratarse de puntos fijos. Y los vectores de velocidad angular {01} y {20} están implícitamente dados en el enunciado (sus direcciones son las de los correspondientes ejes de rotación, sus módulos son constantes y se especifican de forma explícita, y sus sentidos se indican en la figura).

Así, pues, las reducciones cinemáticas canónicas pedidas son las siguientes:

$\left\{\begin{array}{l} \vec{\omega}_{01}(t)=\Omega\,\vec{k}_0 \\ \\ \vec{v}^{\, O}_{01}(t)=\vec{0} \end{array}\right.\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \left\{\begin{array}{l} \vec{\omega}_{20}(t)=-2\,\Omega\,\vec{\imath}_0 \\ \\ \vec{v}^{\, B}_{20}(t)=\vec{0} \end{array}\right.$

3 Velocidades del punto C

Calculamos la velocidad relativa (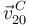 $\vec{v}^{\, C}_{20}\,$ ) y la velocidad de arrastre ( 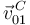$\vec{v}^{\, C}_{01}\,$ ) utilizando las ecuaciones de los campos de velocidades correspondientes, y la velocidad absoluta ( 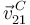$\vec{v}^{\, C}_{21}\,$ ) mediante la ley de composición de velocidades:

$\begin{array}{l} \vec{v}^{\, C}_{20}=\displaystyle\underbrace{\vec{v}^{B}_{20}}_{=\vec{0}}+\,\vec{\omega}_{20}\times\overrightarrow{BC}=-2\,\Omega\,\vec{\imath}_0\times\displaystyle\frac{L}{2}\,\vec{k}_0=\Omega L\,\vec{\jmath}_0 \\ \\ \vec{v}^{\, C}_{01}=\displaystyle\underbrace{\vec{v}^{\, O}_{01}}_{=\vec{0}}+\,\vec{\omega}_{01}\times\overrightarrow{OC}=\Omega\,\vec{k}_0\times\left(-\displaystyle\frac{L}{2}\,\vec{\imath}_0+\displaystyle\frac{L}{2}\,\vec{\jmath}_0+\displaystyle\frac{L}{2}\,\vec{k}_0\right)=-\displaystyle\frac{\Omega L}{2}(\vec{\imath}_0+\vec{\jmath}_0) \\ \\ \vec{v}^{\, C}_{21}=\vec{v}^{\, C}_{20}+\vec{v}^{\, C}_{01}=\displaystyle\frac{\Omega L}{2}(-\vec{\imath}_0+\vec{\jmath}_0) \end{array}$

5.9. Silla giratoria (Ex.Dic/12)

De Laplace

1 Enunciado

2 Reducciones cinemáticas canónicas {01} y {20}

3 Velocidades del punto C

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES